【题目】已知函数f(x)=2sinx+1. (Ⅰ)设ω为大于0的常数,若f(ωx)在区间 ![]() 上单调递增,求实数ω的取值范围;
上单调递增,求实数ω的取值范围;
(Ⅱ)设集合 ![]() ,B={x||f(x)﹣m|<2},若A∪B=B,求实数m的取值范围.
,B={x||f(x)﹣m|<2},若A∪B=B,求实数m的取值范围.
参考答案:
【答案】解:(Ⅰ)由题意,f(ωx)=2sinωx+1,由ωx∈[﹣ ![]() ,
, ![]() ],ω>0,可得x∈[﹣
],ω>0,可得x∈[﹣ ![]() ,
, ![]() ], ∵f(ωx)在区间
], ∵f(ωx)在区间 ![]() 上单调递增,
上单调递增,
∴ 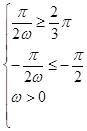 ,
,
∴0<ω≤ ![]() ;
;
(Ⅱ)∵A∪B=B,
∴AB,
∵|f(x)﹣m|<2,
∴m﹣2<f(x)<m+2,
∵ ![]() ,
,
∴ ![]() ,
,
∴2≤f(x)≤3,
∴ ![]() ,
,
∴1<m<4
【解析】(Ⅰ)由题意,f(ωx)=2sinωx+1,由ωx∈[﹣ ![]() ,
, ![]() ],ω>0,可得x∈[﹣
],ω>0,可得x∈[﹣ ![]() ,
, ![]() ],利用f(ωx)在区间
],利用f(ωx)在区间 ![]() 上单调递增,可得不等式组,解不等式组,即可求实数ω的取值范围;(Ⅱ)求出函数的值域,根据A∪B=B,可得AB,从而可得不等式组,解不等式,即可求出实数m的取值范围.
上单调递增,可得不等式组,解不等式组,即可求实数ω的取值范围;(Ⅱ)求出函数的值域,根据A∪B=B,可得AB,从而可得不等式组,解不等式,即可求出实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若Ai(i=1,2,3,…,n)是△AOB所在平面内的点,且
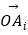
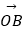 =
= 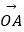
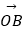 ,给出下列说法:
,给出下列说法:
·(1)|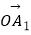 |=|
|=| 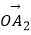 |=|
|=| 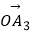 |=…=|
|=…=| 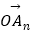 |
|
·(2)|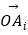 |的最小值一定是|
|的最小值一定是| 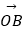 |
|
·(3)点A和点Ai一定共线
·(4)向量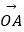 及
及 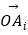 在向量
在向量 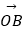 方向上的投影必定相等
方向上的投影必定相等
其中正确的个数是( )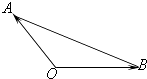
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是R上的奇函数,且当x∈[0,+∞)时,
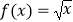 . (Ⅰ)求f(x)的解析式;
. (Ⅰ)求f(x)的解析式;
(Ⅱ)运用函数单调性定义证明f(x)在定义域R上是增函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=loga(1+x),g(x)=loga(1+kx),其中a>0且a≠1. (Ⅰ)当k=﹣2时,求函数h(x)=f(x)+g(x)的定义域;
(Ⅱ)若函数H(x)=f(x)﹣g(x)是奇函数(不为常函数),求实数k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】f(x)=x2﹣2x,g(x)=ax+2(a>0),若对任意的x1∈[﹣1,2],存在x0∈[﹣1,2],使g(x1)=f(x0),则a的取值范围是( )
A.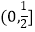
B.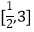
C.[3,+∞)
D.(0,3] -
科目: 来源: 题型:
查看答案和解析>>【题目】某餐厅装修,需要大块胶合板
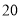 张,小块胶合板
张,小块胶合板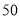 张,已知市场出售
张,已知市场出售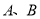 两种不同规格的胶合板。经过测算,
两种不同规格的胶合板。经过测算, 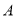 种规格的胶合板可同时截得大块胶合板
种规格的胶合板可同时截得大块胶合板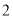 张,小块胶合板
张,小块胶合板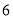 张,
张, 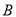 种规格的胶合板可同时截得大块胶合板
种规格的胶合板可同时截得大块胶合板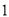 张,小块胶合板
张,小块胶合板 张.已知
张.已知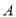 种规格胶合板每张
种规格胶合板每张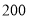 元,
元, 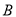 种规格胶合板每张
种规格胶合板每张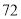 元.分别用
元.分别用 表示购买
表示购买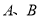 两种不同规格的胶合板的张数.
两种不同规格的胶合板的张数.(1)用
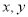 列出满足条件的数学关系式,并画出相应的平面区域;
列出满足条件的数学关系式,并画出相应的平面区域;(2)根据施工需求,
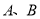 两种不同规格的胶合板各买多少张花费资金最少?并求出最少资金数.
两种不同规格的胶合板各买多少张花费资金最少?并求出最少资金数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正三棱锥P﹣ABC,点P,A,B,C都在半径为
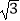 的球面上,若PA,PB,PC两两垂直,则球心到截面ABC的距离为 .
的球面上,若PA,PB,PC两两垂直,则球心到截面ABC的距离为 .
相关试题

