【题目】如图,在三棱柱![]() 中,底面
中,底面![]() 是边长为2的等边三角形,
是边长为2的等边三角形, ![]() 为
为![]() 的中点.
的中点.
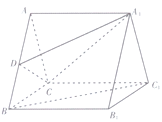
(1)求证: ![]() 平面
平面![]() ;
;
(2)若四边形![]() 是正方形,且
是正方形,且![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
参考答案:
【答案】(1)详见解析(2)![]()
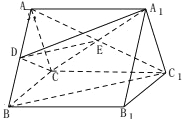
【解析】试题分析:(1)连AC1,设AC1与A1C相交于点O,先利用中位线定理证明DO∥BC1,再利用线面平行的判定定理证明结论即可;(2)推导出三棱柱ABC-A1B1C1是正三棱柱,以C为原点,CB为x轴,CC1为y轴,过C作平面CBB1C1的垂线为z轴,建立空间直角坐标系,利用向量法能求出直线A1D与平面CBB1C1所成角的正弦值
试题解析:(1)证明:连结![]() ,设
,设![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,则
,则![]() 为
为![]() 中点,
中点,
![]() 为
为![]() 的中点,
的中点, ![]() ……2
……2
∴![]() 平面
平面![]() . ……4
. ……4
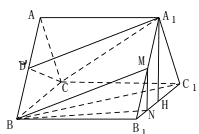
(2)取![]() 的中点
的中点![]() ,连结
,连结![]() ,则
,则![]()
![]() ,故
,故![]() ,∴
,∴![]()
![]()
![]() ,
,![]() 平面
平面![]() ……8
……8
取![]() 中点
中点![]() ,连结
,连结![]() ,过点作
,过点作![]() ,则
,则
连结![]() ,
, ![]() ,
,
![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角, ……10
所成的角, ……10
![]()
即直线![]() 与平面所
与平面所![]() 成的角的正弦值为
成的角的正弦值为![]() . ……12
. ……12
-
科目: 来源: 题型:
查看答案和解析>>【题目】设圆上的点A(2,3)关于直线x+2y=0的对称点仍在圆上,且直线x-y+1=0被圆截得的弦长为2
 ,求圆的方程.
,求圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
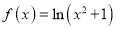 ,
, 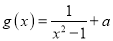
(1)若
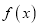 的一个极值点到直线
的一个极值点到直线 的距离为1,求
的距离为1,求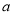 的值;
的值;(2)求方程
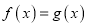 的根的个数
的根的个数 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
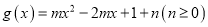 在
在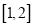 上有最大值1和最小值0,设
上有最大值1和最小值0,设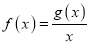 .
.(1)求
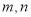 的值;
的值;(2)若不等式
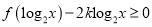 在
在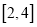 上有解,求实数
上有解,求实数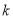 的取值范围;
的取值范围;(3)若方程
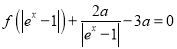 (
(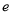 为自然对数的底数)有三个不同的实数解,求实数
为自然对数的底数)有三个不同的实数解,求实数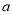 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
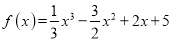 .
.(Ⅰ)求
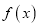 的单调区间;
的单调区间;(Ⅱ)若曲线
 与
与 有三个不同的交点,求实数
有三个不同的交点,求实数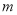 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】2014年3月的“两会”上,李克强总理在政府工作报告中,首次提出“倡导全民阅读”,某学校响应政府倡导,在学生中发起读书热潮.现统计了从2014年下半年以来,学生每半年人均读书量,如下表:
时间
2014年下半年
2015年上半年
2015年下半年
2016年上半年
2016年下半年
时间代号
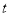
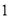
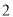
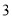
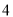
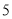
人均读书量
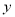 (本)
(本)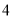
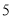
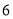
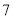
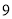
根据散点图,可以判断出人均读书量
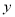 与时间代号
与时间代号 具有线性相关关系.
具有线性相关关系.(1)求
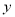 关于
关于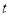 的回归方程
的回归方程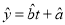 ;
;(2)根据所求的回归方程,预测该校2017年上半年的人均读书量.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
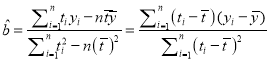 ,
, 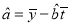
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场进行有奖促销活动,顾客购物每满500元,可选择返回50元现金或参加一次抽奖,抽奖规则如下:从1个装有6个白球、4个红球的箱子中任摸一球,摸到红球就可获得100元现金奖励,假设顾客抽奖的结果相互独立.
(Ⅰ)若顾客选择参加一次抽奖,求他获得100元现金奖励的概率;
(Ⅱ)某顾客已购物1500元,作为商场经理,是希望顾客直接选择返回150元现金,还是选择参加3次抽奖?说明理由;
(Ⅲ)若顾客参加10次抽奖,则最有可能获得多少现金奖励?
相关试题

