【题目】如图,已知直三棱柱ABC﹣A1B1C1中,AB=5,AC=4,BC=3,AA1=4,点D在AB上. 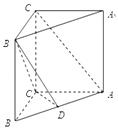
(1)若D是AB中点,求证:AC1∥平面B1CD;
(2)当 ![]() =
= ![]() 时,求二面角B﹣CD﹣B1的余弦值.
时,求二面角B﹣CD﹣B1的余弦值.
参考答案:
【答案】
(1)证明:连接BC1,交B1C于E,连接DE.
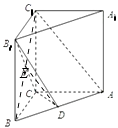
∵ABC﹣A1B1C1是直三棱柱,D是AB中点
∴侧面BB1C1C为矩形,DE为△ABC1的中位线
∴DE∥AC1,
又∵DE平面B1CD,AC1平面B1CD
∴AC1∥平面B1CD.
(2)∵AB=5,AC=4,BC=3,即AB2=AC2+BC2
∴AC⊥BC,所以如图,以C为原点建立空间直角坐标系C﹣xyz.

则B (3,0,0),A (0,4,0),
A1 (0,4,4),B1 (3,0,4).
设D (a,b,0)(a>0,b>0),
∵点D在线段AB上,且 ![]() =
= ![]() ,即
,即 ![]() =
= ![]()
![]()
∴a= ![]() ,b=
,b= ![]()
∴ ![]() =(﹣3,0,﹣4),
=(﹣3,0,﹣4), ![]() =(
=( ![]() ,
, ![]() ,0)
,0)
显然 ![]() =(0,0,4)是平面BCD的一个法向量
=(0,0,4)是平面BCD的一个法向量
设平面B1CD的法向量为 ![]() =(x,y,z),那么
=(x,y,z),那么
由 ![]()
![]() =0,
=0, ![]()
![]() =0,得
=0,得 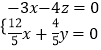 ,
,
令x=1,得 ![]() =(1,﹣3,﹣
=(1,﹣3,﹣ ![]() )
)
∴cos ![]() =
= =
![]() =﹣
=﹣ ![]()
又二面角B﹣CD﹣B1是锐角,故其余项值为 ![]()
【解析】(1)通过作平行线,由线线平行证明线面平行;(2)建立空间直角坐标系,求得两平面的法向量,利用向量法求二面角的余弦值.
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,函数
,函数
(1)讨论函数
 的单调性;
的单调性;(2)若函数
 有两个不同的零点
有两个不同的零点 ,求实数
,求实数 的取值范围;
的取值范围;(3)在(2)的条件下,求证:

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
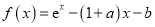 (
(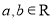 ),其中
),其中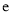 为自然对数的底数.
为自然对数的底数.(1)讨论函数
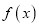 的单调性及极值;
的单调性及极值;(2)若不等式
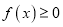 在
在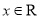 内恒成立,求证:
内恒成立,求证:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知各项均为正数的等比数列{an}的首项a1=2,Sn为其前n项和,若5S1 , S3 , 3S2成等差数列.
(1)求数列{an}的通项公式;
(2)设bn=log2an , cn=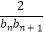 ,记数列{cn}的前n项和为Tn . 若对于任意的n∈N* , Tn≤λ(n+4)恒成立,求实数λ的取值范围.
,记数列{cn}的前n项和为Tn . 若对于任意的n∈N* , Tn≤λ(n+4)恒成立,求实数λ的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,直线
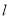 的参数方程为
的参数方程为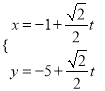 (其中
(其中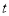 为参数),现以坐标原点为极点,
为参数),现以坐标原点为极点, 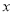 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线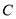 的极坐标方程为
的极坐标方程为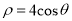 .
.(1)写出直线
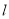 和曲线
和曲线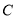 的普通方程;
的普通方程;(2)已知点
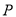 为曲线
为曲线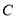 上的动点,求
上的动点,求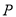 到直线
到直线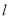 的距离的最小值.
的距离的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中 且
且 ,若
,若 ,
,  在
在 处切线的斜率为
处切线的斜率为 .
.(1)求函数
 的解析式及其单调区间;
的解析式及其单调区间;(2)若实数
 满足
满足 ,且
,且 对于任意
对于任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在数列{an}中,a1=
 ,且
,且 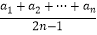 =nan(n∈N+).
=nan(n∈N+).
(1)写出此数列的前4项;
(2)归纳猜想{an}的通项公式,并用数学归纳法加以证明.
相关试题

