【题目】已知函数![]() (
(![]() ),其中
),其中![]() 为自然对数的底数.
为自然对数的底数.
(1)讨论函数![]() 的单调性及极值;
的单调性及极值;
(2)若不等式![]() 在
在![]() 内恒成立,求证:
内恒成立,求证: ![]() .
.
参考答案:
【答案】(1)答案见解析;(2)证明见解析.
【解析】试题分析:
(1)由题意可得导函数的解析式![]() ,分类讨论可得:当
,分类讨论可得:当![]() 时,
时, ![]() 在
在![]() 内单调递增,没有极值;当
内单调递增,没有极值;当![]() 时,
时, ![]() 在区间
在区间![]() 内单调递减,在区间
内单调递减,在区间![]() 内单调递增,
内单调递增, ![]() 的极小值为
的极小值为![]() ,无极大值.
,无极大值.
(2)分类讨论:当![]() 时,
时, ![]() 明显成立;
明显成立;
当![]() 时,由(1),知
时,由(1),知![]() 在
在![]() 内单调递增,此时利用反证法可证得结论;
内单调递增,此时利用反证法可证得结论;
当![]() 时,构造新函数
时,构造新函数![]() ,结合函数的单调性即可证得题中的结论.
,结合函数的单调性即可证得题中的结论.
试题解析:
(1)由题意得![]() .
.
当![]() ,即
,即![]() 时,
时, ![]() ,
, ![]() 在
在![]() 内单调递增,没有极值.
内单调递增,没有极值.
当![]() ,即
,即![]() 时,
时,
令![]() ,得
,得![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() ,
, ![]() 单调递增,
单调递增,
故当![]() 时,
时, ![]() 取得极小值
取得极小值![]()
![]() ,无极大值.
,无极大值.
综上所述,当![]() 时,
时, ![]() 在
在![]() 内单调递增,没有极值;
内单调递增,没有极值;
当![]() 时,
时, ![]() 在区间
在区间![]() 内单调递减,在区间
内单调递减,在区间![]() 内单调递增,
内单调递增, ![]() 的极小值为
的极小值为![]() ,无极大值.
,无极大值.
(2)当![]() 时,
时, ![]() 成立.
成立.
当![]() 时,由(1),知
时,由(1),知![]() 在
在![]() 内单调递增,
内单调递增,
令![]() 为
为![]() 和
和![]() 中较小的数,
中较小的数,
所以![]() ,且
,且![]() ,
,
则![]() ,
, ![]() .
.
所以![]()
![]() ,
,
与![]() 恒成立矛盾,应舍去.
恒成立矛盾,应舍去.
当![]() 时,
时, ![]()
![]() ,
,
即![]() ,
,
所以![]() .
.
令![]() ,
,
则![]() .
.
令![]() ,得
,得![]() ,
,
令![]() ,得
,得![]() ,
,
故![]() 在区间
在区间![]() 内单调递增,
内单调递增,
在区间![]() 内单调递减.
内单调递减.
故![]() ,
,
即当![]() 时,
时, ![]() .
.
所以![]()
![]() .
.
所以![]() .
.
而![]() ,
,
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对定义域分别为D1 , D2的函数y=f(x),y=g(x),规定:函数h(x)=
 ,f(x)=x﹣2(x≥1),g(x)=﹣2x+3(x≤2),则h(x)的单调减区间是
,f(x)=x﹣2(x≥1),g(x)=﹣2x+3(x≤2),则h(x)的单调减区间是 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某城市有一条公路正西方AO通过市中心O后转向北偏东α角方向的OB,位于该市的某大学M与市中心O的距离OM=3
 km,且∠AOM=β,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,且经过大学M,其中tanα=2,cosβ=
km,且∠AOM=β,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,且经过大学M,其中tanα=2,cosβ= 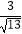 ,AO=15km.
,AO=15km. 
(1)求大学M在站A的距离AM;
(2)求铁路AB段的长AB. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,函数
,函数
(1)讨论函数
 的单调性;
的单调性;(2)若函数
 有两个不同的零点
有两个不同的零点 ,求实数
,求实数 的取值范围;
的取值范围;(3)在(2)的条件下,求证:

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知各项均为正数的等比数列{an}的首项a1=2,Sn为其前n项和,若5S1 , S3 , 3S2成等差数列.
(1)求数列{an}的通项公式;
(2)设bn=log2an , cn=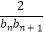 ,记数列{cn}的前n项和为Tn . 若对于任意的n∈N* , Tn≤λ(n+4)恒成立,求实数λ的取值范围.
,记数列{cn}的前n项和为Tn . 若对于任意的n∈N* , Tn≤λ(n+4)恒成立,求实数λ的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直三棱柱ABC﹣A1B1C1中,AB=5,AC=4,BC=3,AA1=4,点D在AB上.
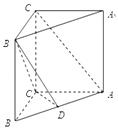
(1)若D是AB中点,求证:AC1∥平面B1CD;
(2)当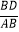 =
= 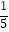 时,求二面角B﹣CD﹣B1的余弦值.
时,求二面角B﹣CD﹣B1的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,直线
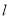 的参数方程为
的参数方程为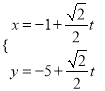 (其中
(其中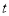 为参数),现以坐标原点为极点,
为参数),现以坐标原点为极点, 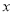 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线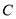 的极坐标方程为
的极坐标方程为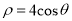 .
.(1)写出直线
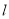 和曲线
和曲线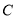 的普通方程;
的普通方程;(2)已知点
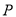 为曲线
为曲线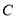 上的动点,求
上的动点,求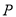 到直线
到直线 的距离的最小值.
的距离的最小值.
相关试题

