【题目】已知函数f(x)=log4(4x+1)+2kx(k∈R)是偶函数.
(1)求k的值;
(2)若方程f(x)=m有解,求m的取值范围.
参考答案:
【答案】
(1)解:由函数f(x)是偶函数可知,f(﹣x)=f(x),
∴log4(4x+1)+2kx=log4(4﹣x+1)﹣2kx,即log4 ![]() =﹣4kx,
=﹣4kx,
∴log44x=﹣4kx,∴x=﹣4kx,即(1+4k)x=0,对一切x∈R恒成立,
∴k=﹣ ![]()
(2)解:由m=f(x)=log4(4x+1)﹣ ![]() x=log4
x=log4 ![]() =log4(2x+
=log4(2x+ ![]() ),
),
∵2x>0,∴2x+ ![]() ≥2,∴m≥log42=
≥2,∴m≥log42= ![]() .
.
故要使方程f(x)=m有解,
m的取值范围为[ ![]() ,+∞)
,+∞)
【解析】(1)利用函数是偶函数,利用定义推出方程求解即可.(2)通过方程有解,求出函数的最值,即可推出m的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2﹣4x+a+3,a∈R.
(1)若函数y=f(x)的图象与x轴无交点,求a的取值范围;
(2)若函数y=f(x)在[﹣1,1]上存在零点,求a的取值范围;
(3)设函数g(x)=bx+5﹣2b,b∈R.当a=0时,若对任意的x1∈[1,4],总存在x2∈[1,4],使得f(x1)=g(x2),求b的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】“城中观海”是近年来国内很多大中型城市内涝所致的现象,究其原因,除天气因素、城市规划等原因外,城市垃圾杂物也是造成内涝的一个重要原因.暴雨会冲刷城市的垃圾杂物一起进入下水道,据统计,在不考虑其它因素的条件下,某段下水道的排水量V(单位:立方米/小时)是杂物垃圾密度x(单位:千克/立方米)的函数.当下水道的垃圾杂物密度达到2千克/立方米时,会造成堵塞,此时排水量为0;当垃圾杂物密度不超过0.2千克/立方米时,排水量是90立方米/小时;研究表明,0.2≤x≤2时,排水量V是垃圾杂物密度x的一次函数.
(1)当0≤x≤2时,求函数V(x)的表达式;
(2)当垃圾杂物密度x为多大时,垃圾杂物量(单位时间内通过某段下水道的垃圾杂物量,单位:千克/小时)f(x)=xV(x)可以达到最大,求出这个最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
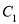 :
: 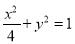 ,曲线
,曲线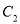 上的动点
上的动点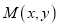 满足:
满足: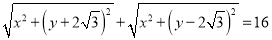 .
.(1)求曲线
 的方程;
的方程;(2)设
 为坐标原点,第一象限的点
为坐标原点,第一象限的点 分别在
分别在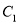 和
和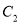 上,
上, 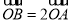 ,求线段
,求线段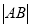 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 (m∈Z)为偶函数,且在(0,+∞)上为增函数.
(m∈Z)为偶函数,且在(0,+∞)上为增函数.
(1)求m的值,并确定f(x)的解析式;
(2)若g(x)=loga[f(x)﹣ax](a>0且a≠1),是否存在实数a,使g(x)在区间[2,3]上的最大值为2,若存在,求出a的值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】连掷一枚均匀的骰子两次,所得向上的点数分别为
 ,记
,记 ,则下列说法正确的是( )
,则下列说法正确的是( )A. 事件“
 ”的概率为
”的概率为 B. 事件“
B. 事件“ 是奇数”与“
是奇数”与“ ”互为对立事件
”互为对立事件C. 事件“
 ”与“
”与“ ”互为互斥事件 D. 事件“
”互为互斥事件 D. 事件“ ”的概率为
”的概率为
-
科目: 来源: 题型:
查看答案和解析>>【题目】A={x|x2﹣2x﹣8<0},B={x|x2+2x﹣3>0},C={x|x2﹣3ax+2a2<0},
(1)求A∩B.
(2)试求实数a的取值范围,使C(A∩B).
相关试题

