【题目】为宣传3月5日学雷锋纪念日,重庆二外在高一,高二年级中举行学雷锋知识竞赛,每年级出3人组成甲乙两支代表队,首轮比赛每人一道必答题,答对则为本队得1分,答错不答都得0分,已知甲队3人每人答对的概率分别为![]() ,乙队每人答对的概率都是
,乙队每人答对的概率都是![]() .设每人回答正确与否相互之间没有影响,用
.设每人回答正确与否相互之间没有影响,用![]() 表示甲队总得分.
表示甲队总得分.
(1)求随机变量![]() 的分布列及其数学期望
的分布列及其数学期望![]() ;
;
(2)求甲队和乙队得分之和为4的概率.
参考答案:
【答案】(1)分布列详见解析, ![]() (2)
(2)![]()
【解析】试题分析:
(1) ![]() 的可能取值为0,1,2,3,求得相应的概率值即可得到分布列和数学期望;
的可能取值为0,1,2,3,求得相应的概率值即可得到分布列和数学期望;
(2)结合题意可知满足题意的事件为“甲队3分且乙队1分”,“甲队2分且乙队2分”,“甲队1分且乙队3分”三个基本事件,据此可得概率值为![]() .
.
试题解析:
解:(1)![]() 的可能取值为0,1,2,3.
的可能取值为0,1,2,3.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() .
.
(2)设“甲队和乙队得分之和为4”事件A,包含“甲队3分且乙队1分”,“甲队2分且乙队2分”,“甲队1分且乙队3分”三个基本事件,则:
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题p:x>0,x+
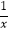 >a;命题q:x0∈R,x02﹣2ax0+1≤0.若¬q为假命题,p∧q为假命题,则求a的取值范围.
>a;命题q:x0∈R,x02﹣2ax0+1≤0.若¬q为假命题,p∧q为假命题,则求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):
规定若满意度不低于98分,测评价该教师为“优秀”.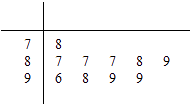
(1)求从这10人中随机选取3人,至多有1人评价该教师是“优秀”的概率;
记ξ表示抽到评价该教师为“优秀”的人数,求ξ的分布列及数学期望.
(2)以这10人的样本数据来估计整个班级的总体数据,若从该班任选3人, -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱ABC﹣A1B1C1中,点D是BC的中点.

(1)求证:A1B∥平面ADC1;
(2)若AB⊥AC,AB=AC=1,AA1=2,求平面ADC1与ABA1所成二面角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
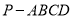 中,
中,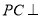 底面
底面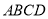 ,底面
,底面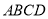 是直角梯形,
是直角梯形,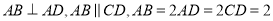 ,
,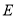 是
是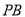 上的点.
上的点.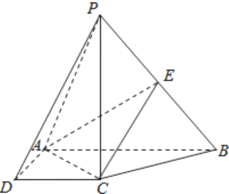
(1)求证: 平面
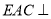 平面
平面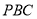 ;
; (2)若
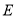 是
是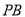 的中点,且二面角
的中点,且二面角 的余弦值为
的余弦值为 ,求直线
,求直线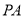 与平面
与平面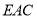 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
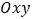 中,已知点
中,已知点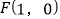 和直线
和直线 :
: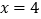 ,圆C与直线
,圆C与直线 相切,并且圆心C关于点
相切,并且圆心C关于点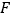 的对称点在圆C上,直线
的对称点在圆C上,直线 与
与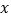 轴相交于点
轴相交于点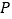 .
.(Ⅰ)求圆心C的轨迹E的方程;
(Ⅱ)过点
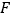 且与直线
且与直线 不垂直的直线
不垂直的直线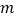 与圆心C的轨迹E相交于点A、B,求
与圆心C的轨迹E相交于点A、B,求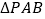 面积的取值范围.
面积的取值范围. -
科目: 来源: 题型:
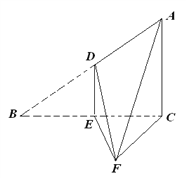
查看答案和解析>>【题目】如图,直角
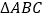 中,∠
中,∠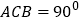 ,
,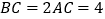 ,D、E分别是AB、BC边的中点,沿DE将
,D、E分别是AB、BC边的中点,沿DE将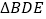 折起至
折起至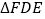 ,且∠
,且∠ .
.(Ⅰ)求四棱锥F-ADEC的体积;
(Ⅱ)求证:平面ADF⊥平面ACF.
相关试题

