【题目】如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E.求证:DA=DE.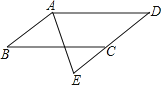
参考答案:
【答案】证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠E=∠BAE,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠E=∠DAE,
∴DA=DE.
【解析】由平行四边形的性质得出AB∥CD,得出内错角相等∠E=∠BAE,再由角平分线证出∠E=∠DAE,即可得出结论.本题考查了平行四边形的性质、平行线的性质、等腰三角形的判定;熟练掌握平行四边形的性质,证出∠E=∠DAE是解决问题的关键.
【考点精析】关于本题考查的平行四边形的性质,需要了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】毕节市正实施“五城同创”计划。为搞好卫生维护工作,政府招聘了200名市民志愿者,按年龄情况进行统计的频率分布表和频率分布直方图如下:
分组(岁)
频数
频率
[30,35)
20
0.1
[35,40)
20
0.1
[40,45)
①
0.2
[45,50)
②
③
[50,55]
40
0.2
合计
200
1
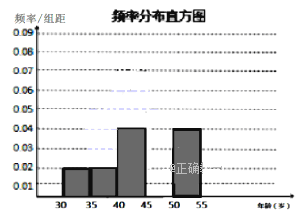
(1)频率分布表中的①②③位置应填什么数?补全频率分布直方图;
(2)根据频率分布直方图估计这200名志愿者的平均年龄.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
设函数
 ,
, .
.(Ⅰ)当
 时,求函数
时,求函数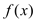 的极小值;
的极小值;(Ⅱ)讨论函数
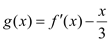 零点的个数;
零点的个数;(Ⅲ)若对任意的
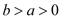 ,
,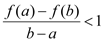 恒成立,求
恒成立,求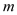 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
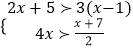 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直三棱柱
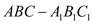 中,
中, ,
, ,
, ,
, ,点
,点 在线段
在线段 上.
上.
(Ⅰ)证明
 ;
;(Ⅱ)若
 是
是 中点,证明
中点,证明 平面
平面 ;
;(Ⅲ)当
 时,求二面角
时,求二面角 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名篮球运动员互不影响地在同一位置投球,命中率分别为
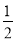 与
与 ,且乙投球2次均未命中的概率为
,且乙投球2次均未命中的概率为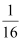 。
。(1)求乙投球的命中率
 。
。(2)若甲投球1次,乙投球2次,两人共命中的次数记为
 ,求
,求 的分布列和数学期望。
的分布列和数学期望。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:x2+y2-2x+4y-4=0,
(1)求圆C关于直线
 对称的圆的方程;
对称的圆的方程;(2)问是否存在斜率为1的直线l,使l被圆C截得弦AB,且以AB为直径的圆经过点
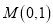 ?若存在,求出直线l的方程;若不存在,说明理由.
?若存在,求出直线l的方程;若不存在,说明理由.
相关试题

