【题目】已知函数g(x)满足g(x)=g′(1)ex﹣1﹣g(0)x+ ![]() ,且存在实数x0使得不等式2m﹣1≥g(x0)成立,则m的取值范围为( )
,且存在实数x0使得不等式2m﹣1≥g(x0)成立,则m的取值范围为( )
A.(﹣∞,2]
B.(﹣∞,3]
C.[1,+∞)
D.[0,+∞)
参考答案:
【答案】C
【解析】解:∵g(x)=g′(1)ex﹣1﹣g(0)x+ ![]() ,
,
∴g′(x)=g′(1)ex﹣1﹣g(0)+x,
∴g′(1)=g′(1)﹣g(0)+1,解得:g(0)=1,
g(0)=g′(1)e﹣1 , 解得:g′(1)=e,
∴g(x)=ex﹣x+ ![]() x2 ,
x2 ,
∴g′(x)=ex﹣1+x,g″(x)=ex+1>0,
∴g′(x)在R递增,而g′(0)=0,
∴g′(x)<0在(﹣∞,0)恒成立,g′(x)>0在(0,+∞)恒成立,
∴g(x)在(﹣∞,0)递减,在(0,+∞)递增,
∴g(x)min=g(0)=1,
若存在实数x0使得不等式2m﹣1≥g(x0)成立,
只需2m﹣1≥g(x)min=1即可,解得:m≥1,
故选:C.
分别求出g(0),g′(1),求出g(x)的表达式,求出g(x)的导数,得到函数的单调区间,求出g(x)的最小值,问题转化为只需2m﹣1≥g(x)min=1即可,求出m的范围即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司过去五个月的广告费支出x与销售额y(单位:万元)之间有下列对应数据:
x
2
4
5
6
8
y

40
60
50
70
工作人员不慎将表格中y的第一个数据丢失.已知y对x呈线性相关关系,且回归方程为
 =6.5x+17.5,则下列说法:
=6.5x+17.5,则下列说法:
①销售额y与广告费支出x正相关;
②丢失的数据(表中 处)为30;
处)为30;
③该公司广告费支出每增加1万元,销售额一定增加6.5万元;
④若该公司下月广告投入8万元,则销售额为70万元.
其中,正确说法有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0)的一系列对应值如表:
x
﹣


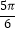
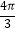
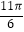
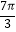
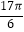
y
﹣1
1
3
1
﹣1
1
3
(1)根据表格提供的数据求函数f(x)的一个解析式;
(2)根据(1)的结果:
( i)当x∈[0, ]时,方程f(3x)=m恰有两个不同的解,求实数m的取值范围;
]时,方程f(3x)=m恰有两个不同的解,求实数m的取值范围;
( ii)若α,β是锐角三角形的两个内角,试比较f(sinα)与f(cosβ)的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列an}的前n项和为Sn , a1=1,a2=2,且点(Sn , Sn+1)在直线y=tx+1上.
(1)求Sn及an;
(2)若数列{bn}满足bn=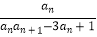 (n≥2),b1=1,数列{bn}的前n项和为Tn , 求证:当n≥2时,Tn<2.
(n≥2),b1=1,数列{bn}的前n项和为Tn , 求证:当n≥2时,Tn<2. -
科目: 来源: 题型:
查看答案和解析>>【题目】记集合A={(x,y)|x2+y2≤16}和集合B={(x,y)|x+y﹣4≤0,x≥0,y≥0}表示的平面区域分别为Ω1 , Ω2 , 若在区域Ω1内任取一点M(x,y),则点M落在区域Ω2的概率为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数据x1 , x2 , x3 , …,x100是杭州市100个普通职工的2016年10月份的收入(均不超过2万元),设这100个数据的中位数为x,平均数为y,方差为z,如果再加上马云2016年10月份的收入x101(约100亿元),则相对于x、y、z,这101个月收入数据( )
A.平均数可能不变,中位数可能不变,方差可能不变
B.平均数大大增大,中位数可能不变,方差也不变
C.平均数大大增大,中位数一定变大,方差可能不变
D.平均数大大增大,中位数可能不变,方差变大 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解一个英语教改实验班的情况,举行了一次测试,将该班30位学生的英语成绩进行统计,得图示频率分布直方图,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
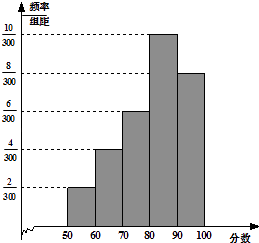
(1)求出该班学生英语成绩的众数,平均数及中位数;
(2)从成绩低于80分的学生中随机抽取2人,规定抽到的学生成绩在[50,60)的记1绩点分,在[60,80)的记2绩点分,设抽取2人的总绩点分为ξ,求ξ的分布列.
相关试题

