【题目】某校为了解一个英语教改实验班的情况,举行了一次测试,将该班30位学生的英语成绩进行统计,得图示频率分布直方图,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]. 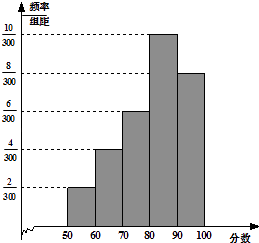
(1)求出该班学生英语成绩的众数,平均数及中位数;
(2)从成绩低于80分的学生中随机抽取2人,规定抽到的学生成绩在[50,60)的记1绩点分,在[60,80)的记2绩点分,设抽取2人的总绩点分为ξ,求ξ的分布列.
参考答案:
【答案】
(1)解:由频率分布直方图可知:众数为85.
平均数为:55× ![]() =81,
=81,
∴该班学生英语成绩的平均数为81.
设中位数为x,由频率分布直方图,得:
[50,80)内的频率为( ![]() )×10=0.4,[80,90)内的频率为
)×10=0.4,[80,90)内的频率为 ![]() =
= ![]() ,
,
∴中位数x=80+ ![]() =83.
=83.
(2)解:依题意,成绩在[50,60)的学生数为30× ![]() ,
,
成绩在[60,80)的学生数为30× ![]() =10,
=10,
∴成绩低于80分的学生总人数为 12,
∴ξ可取的值为2,3,4,
P(ξ=2)= ![]() =
= ![]() ,
,
P(ξ=3)= ![]() =
= ![]() ,
,
P(ξ=4)= ![]() =
= ![]() ,
,
∴ξ的分布列为:
ξ | 2 | 3 | 4 |
P |
|
|
|
∴ξ的数学期望E(ξ)=2× ![]() =
= ![]() .
.
【解析】(1)由频率分布直方图能求出众数、平均数和中位数.(2)依题意,成绩在[50,60)的学生数为2人,成绩在[60,80)的学生数为10人,ξ可取的值为2,3,4,分别求出相应的概率,由此能求出ξ的分布列和数学期望.
【考点精析】根据题目的已知条件,利用频率分布直方图和离散型随机变量及其分布列的相关知识可以得到问题的答案,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息;在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数g(x)满足g(x)=g′(1)ex﹣1﹣g(0)x+
 ,且存在实数x0使得不等式2m﹣1≥g(x0)成立,则m的取值范围为( )
,且存在实数x0使得不等式2m﹣1≥g(x0)成立,则m的取值范围为( )
A.(﹣∞,2]
B.(﹣∞,3]
C.[1,+∞)
D.[0,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】记集合A={(x,y)|x2+y2≤16}和集合B={(x,y)|x+y﹣4≤0,x≥0,y≥0}表示的平面区域分别为Ω1 , Ω2 , 若在区域Ω1内任取一点M(x,y),则点M落在区域Ω2的概率为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数据x1 , x2 , x3 , …,x100是杭州市100个普通职工的2016年10月份的收入(均不超过2万元),设这100个数据的中位数为x,平均数为y,方差为z,如果再加上马云2016年10月份的收入x101(约100亿元),则相对于x、y、z,这101个月收入数据( )
A.平均数可能不变,中位数可能不变,方差可能不变
B.平均数大大增大,中位数可能不变,方差也不变
C.平均数大大增大,中位数一定变大,方差可能不变
D.平均数大大增大,中位数可能不变,方差变大 -
科目: 来源: 题型:
查看答案和解析>>【题目】运行如图所示的程序框图,若输出的结果为
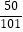 ,则判断框内可以填( )
,则判断框内可以填( ) 
A.k>98?
B.k≥99?
C.k≥100?
D.k>101? -
科目: 来源: 题型:
查看答案和解析>>【题目】某媒体对“男女延迟退休”这一公众关注的问题进行了民意调查,如表是在某单位得到的数据(人数):
(1)能否有90%以上的把握认为对这一问题的看法与性别有关?赞同
反对
合计
男
5
6
11
女
11
3
14
合计
16
9
25
(2)从赞同“男女延迟退休”16人中选出3人进行陈 述发言,求事件“男士和女士各至少有1人发言”的概率;
(3)若以这25人的样本数据来估计整个地区的总体数据,现从该地区(人数很多)任选5人,记赞同“男女延迟退休”的人数为X,求X的数学期望.
附:p(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
K2=
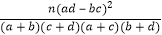 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】天气预报说,未来三天每天下雨的概率都是0.6,用1、2、3、4表示不下雨,用5、6、7、8、9、0表示下雨,利用计算机生成下列20组随机数,则未来三天恰有两天下雨的概率大约是 .
757 220 582 092 103 000 181 249 414 993
010 732 680 596 761 835 463 521 186 289.
相关试题

