【题目】某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为![]() 、
、![]() 、
、![]() 三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).


(Ⅰ)根据规定,该产品各工种保单的期望利润都不得超过保费的20%,试分别确定各类工种每张保单保费的上限;
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以(Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.
参考答案:
【答案】(Ⅰ)见解析;(Ⅱ)![]() 元.
元.
【解析】试题分析:(I)设工种![]() 每份保单的保费,则需赔付时,收入为
每份保单的保费,则需赔付时,收入为![]() ,根据概率分布可计算出保费的期望值为
,根据概率分布可计算出保费的期望值为![]() ,令
,令![]() 解得
解得![]() .同理可求得工种
.同理可求得工种![]() 保费的期望值;(II)按照每个工种的人数计算出份数然后乘以(1)得到的期望值,即为总的利润.
保费的期望值;(II)按照每个工种的人数计算出份数然后乘以(1)得到的期望值,即为总的利润.
试题解析:
(Ⅰ)设工种![]() 的每份保单保费为
的每份保单保费为![]() 元,设保险公司每单的收益为随机变量
元,设保险公司每单的收益为随机变量![]() ,则
,则![]() 的分布列为
的分布列为
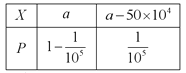
保险公司期望收益为![]()
![]()
![]()
根据规则![]()
解得![]() 元,
元,
设工种![]() 的每份保单保费为
的每份保单保费为![]() 元,赔付金期望值为
元,赔付金期望值为![]() 元,则保险公司期望利润为
元,则保险公司期望利润为![]() 元,根据规则
元,根据规则![]() ,解得
,解得![]() 元,
元,
设工种![]() 的每份保单保费为
的每份保单保费为![]() 元,赔付金期望值为
元,赔付金期望值为![]() 元,则保险公司期望利润为
元,则保险公司期望利润为![]() 元,根据规则
元,根据规则![]() ,解得
,解得![]() 元.
元.
(Ⅱ)购买![]() 类产品的份数为
类产品的份数为![]() 份,
份,
购买![]() 类产品的份数为
类产品的份数为![]() 份,
份,
购买![]() 类产品的份数为
类产品的份数为![]() 份,
份,
企业支付的总保费为![]()
![]()
![]() 元,
元,
保险公司在这宗交易中的期望利润为![]() 元.
元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
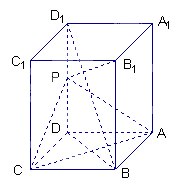
(1)求证:直线BD1∥平面PAC;
(2)求证:直线PB1⊥平面PAC.
(3)求三棱锥B﹣PAC的体积. -
科目: 来源: 题型:
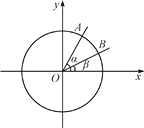
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为
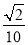 ,
, 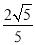 .求:
.求:(1)tan(α+β)的值;
(2)α+2β的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,曲线
中,曲线 :
:  ,曲线
,曲线 :
:  (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点,  轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.(Ⅰ)求曲线
 ,
,  的极坐标方程;
的极坐标方程;(Ⅱ)曲线
 :
:  (
( 为参数,
为参数,  ,
,  )分别交
)分别交 ,
,  于
于 ,
,  两点,当
两点,当 取何值时,
取何值时,  取得最大值.
取得最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
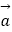 =(sin
=(sin 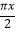 ,sin
,sin  ),
), 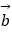 =(cos
=(cos 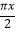 ,cos
,cos  ),且向量
),且向量 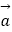 与向量
与向量 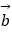 共线.
共线.
(1)求证:sin(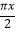 ﹣
﹣  )=0;
)=0;
(2)若记函数f(x)=sin(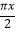 ﹣
﹣  ),求函数f(x)的对称轴方程;
),求函数f(x)的对称轴方程;
(3)求f(1)+f(2)+f(3)+…+f(2013)的值;
(4)如果已知角0<A<B<π,且A+B+C=π,满足f(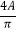 )=f(
)=f( 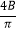 )=
)=  ,求
,求 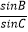 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设在平面上有两个向量a=(cos 2α,sin 2α)(0≤α<π),b=
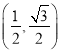 ,a与b不共线.
,a与b不共线.(1)求证:向量a+b与a-b垂直;
(2)当向量
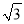 a+b与a-
a+b与a-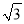 b的模相等时,求α的大小.
b的模相等时,求α的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在底面是矩形的四棱锥PABCD中,PA⊥平面ABCD,PA = AB = 2,BC = 4, E是PD的中点,
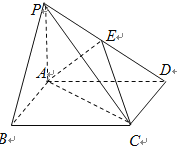
(1)求证:
 平面EAC;
平面EAC; (2)求证:平面PDC⊥平面PAD;
(3)求多面体
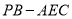 的体积.
的体积.
相关试题

