【题目】通过研究学生的学习行为,心理学家发现,学生接受能力依赖于老师引入概念和描述问题所用的时间,讲座开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持理想的状态,随后学生的注意力开始分散,分析结果和实验表明,用![]() 表示学生掌握和接受概念的能力(
表示学生掌握和接受概念的能力(![]() 的值越大,表示接受能力越强),
的值越大,表示接受能力越强),![]() 表示提出和讲授概念的时间(单位:分),可以有以下公式:
表示提出和讲授概念的时间(单位:分),可以有以下公式: 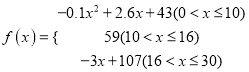 .
.
(1)开讲多少分钟后,学生的接受能力最强?能维持多少分钟?
(2)开讲5分钟与开讲20分钟比较,学生的接受能力何时强一些?
(3)一个数学难题,需要55的接受能力以及13分钟的时间,老师能否及时在学生一直达到所需接受能力的状态下讲授完这个难题?
参考答案:
【答案】(1)能维持6分钟时间(2)开讲5分钟时学生的接受能力比开讲20分钟时要强一些(3)来不及
【解析】试题分析:(1)当![]() 时,函数为二次函数,对称轴为
时,函数为二次函数,对称轴为![]() ,开口向下故在这个区间上单调递增,当
,开口向下故在这个区间上单调递增,当![]() 时取得最大值为
时取得最大值为![]() .当
.当![]() 时,函数为减函数,且
时,函数为减函数,且![]() ,故开讲
,故开讲![]() 分钟后达到最大值,维持
分钟后达到最大值,维持![]() 分钟.(2)通过比较
分钟.(2)通过比较![]() 的值可知开讲
的值可知开讲![]() 分钟时接受能力更强.(3)在区间
分钟时接受能力更强.(3)在区间![]() 上分别令函数值为
上分别令函数值为![]() ,求得对应的时间,作差后可知老师来不及讲授完.
,求得对应的时间,作差后可知老师来不及讲授完.
试题解析:
(1)当![]() 时,
时, ![]()
故![]() 在
在![]() 时递增,最大值为
时递增,最大值为![]()
当![]() 时,
时, ![]()
当![]() 时,
时, ![]() 为减函数,且
为减函数,且![]()
因此,开讲10分钟后,学生达到最强接受能力(为59),能维持6分钟时间.
(2)![]()
![]()
故开讲5分钟时学生的接受能力比开讲20分钟时要强一些
(3)当![]() 时,令
时,令![]() ,解得
,解得![]() 或20(舍)
或20(舍)
当![]() 时,令
时,令![]() ,解得
,解得![]()
因此学生达到(含超过)55的接受能力的时间为![]() (分)
(分)
老师来不及在学生一直达到所需接受能力的状态下讲授完这个难题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的中心为原点
的中心为原点 ,离心率
,离心率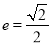 ,其中一个焦点的坐标为
,其中一个焦点的坐标为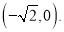
(Ⅰ)求椭圆
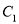 的标准方程;
的标准方程;(Ⅱ)当点
 在椭圆
在椭圆 上运动时,设动点
上运动时,设动点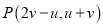 的运动轨迹为
的运动轨迹为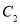 若点
若点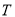 满足:
满足: 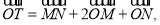 其中
其中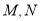 是
是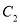 上的点.直线
上的点.直线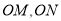 的斜率之积为
的斜率之积为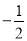 ,试说明:是否存在两个定点
,试说明:是否存在两个定点 ,使得
,使得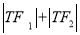 为定值?若存在,求
为定值?若存在,求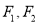 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:人们对声音有不同的感觉,这与它的强度有关系.声音的强度
 用瓦/米2 (
用瓦/米2 (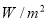 )表示,但在实际测量时,常用声音的强度水平
)表示,但在实际测量时,常用声音的强度水平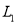 表示,它们满足以下公式:
表示,它们满足以下公式: 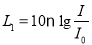 (单位为分贝,
(单位为分贝, 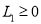 ,其中
,其中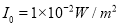 ,这是人们平均能听到的最小强度,是听觉的开端).回答以下问题:
,这是人们平均能听到的最小强度,是听觉的开端).回答以下问题:(1)树叶沙沙声的强度是
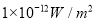 ,耳语的强度是
,耳语的强度是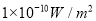 ,恬静的无线电广播的强度是
,恬静的无线电广播的强度是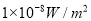 ,试分别求出它们的强度水平;
,试分别求出它们的强度水平;(2)某一新建的安静小区规定:小区内公共场所的声音的强度水平必须保持在50分贝以下,试求声音强度
 的范围为多少?
的范围为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|2x-1|+|x-2a|.
(1)当a=1时,求f(x)≤3的解集;
(2)当x∈[1,2]时,f(x)≤3恒成立,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂今年拟举行促销活动,经调查测算,该厂产品的年销售量(即该厂的年产量)x(万件)与年促销费m(万元)(m≥0)满足x=3-
 .已知今年生产的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
.已知今年生产的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).(1)将今年该产品的利润y(万元)表示为年促销费m(万元)的函数;
(2)求今年该产品利润的最大值,此时促销费为多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
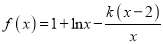 ,其中
,其中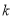 为常数.
为常数.(1)若
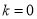 ,求曲线
,求曲线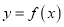 在点
在点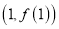 处的切线方程;
处的切线方程;(2)若
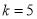 ,求
,求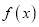 零点的个数;
零点的个数;(3)若
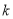 为整数,且当
为整数,且当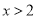 时,
时, 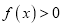 恒成立,求
恒成立,求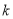 的最大值.
的最大值.(参考数据
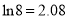 ,
, 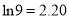 ,
, 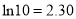 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】设A={x|x2+8x=0},B={x|x2+2(a+2)x+a2-4=0},其中a∈R.如果A∩B=B,求实数a的取值范围.
相关试题

