【题目】一个圆锥的底面半径为2,高为6,在其中有一个高为x的内接圆柱.
(1)用x表示圆柱的轴截面面积S;
(2)当x为何值时,S最大?
参考答案:
【答案】(1) S=-![]() x2+4x(0<x<6).
x2+4x(0<x<6).
(2) 当x=3时,S最大,最大值为6.
【解析】分析:(1)画出圆锥的轴截面,将空间问题转化为平面问题,然后根据相似三角形的性质和比例的性质,得出内接圆柱底面半径r与x关系式即可
(2)根据二次函数的性质易得到其最大值,及对应的x的值.
详解:
画出圆柱和圆锥的轴截面,
如图所示,
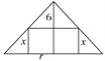
设圆柱的底面半径为r,则由三角形相似可得
![]() =
=![]() ,解得r=2-
,解得r=2-![]() .
.
(1)圆柱的轴截面面积
S=2r·x=2·(2-![]() )·x=-
)·x=-![]() x2+4x(0<x<6).
x2+4x(0<x<6).
(2)∵S=-![]() x2+4x=-
x2+4x=-![]() (x2-6x)
(x2-6x)
=-![]() (x-3)2+6,
(x-3)2+6,
∴当x=3时,S最大,最大值为6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四个命题:
①“若
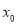 为
为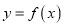 的极值点,则
的极值点,则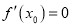 ”的逆命题为真命题;
”的逆命题为真命题; ②“平面向量
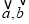 的夹角是钝角”的充分不必要条件是
的夹角是钝角”的充分不必要条件是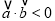
③若命题
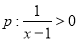 ,则
,则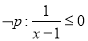
④函数
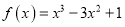 在点
在点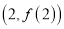 处的切线方程为
处的切线方程为 .
.其中不正确的个数是
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分,(1)小问7分,(2)小问5分)
设函数

(1)若
 在
在 处取得极值,确定
处取得极值,确定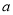 的值,并求此时曲线
的值,并求此时曲线 在点
在点 处的切线方程;
处的切线方程;(2)若
 在
在 上为减函数,求
上为减函数,求 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】若圆(x-1)2+(y+1)2=R2上有且仅有两个点到直线4x+3y=11的距离等于1,则半径R的取值范围是( )
A. R>1 B. R<3 C. 1<R<3 D. R≠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
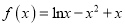
(Ⅰ)求函数
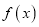 的单调区间;
的单调区间;(Ⅱ)证明当
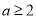 时,关于
时,关于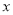 的不等式
的不等式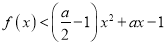 恒成立;
恒成立; -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三棱台ABC﹣A1B1C1中,平面BB1C1C⊥平面ABC,∠ACB=90°,BB1=CC1=B1C1=2,BC=4,AC=6

(1)求证:BC1⊥平面AA1C1C
(2)点D是B1C1的中点,求二面角A1﹣BD﹣B1的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆的一个顶点为A(0,-1),焦点在x轴上。若右焦点F到直线x-y+2
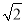 =0的距离为3。
=0的距离为3。(1)求椭圆的方程;
(2)设直线y=kx+m(k≠0)与椭圆相交于不同的两点M、N。当|AM|=|AN|时,求m的取值范围。
相关试题

