【题目】已知实数![]() ,
,![]() 满足
满足![]() ,实数
,实数![]() ,
,![]() 满足
满足![]() ,则
,则![]() 的最小值为__________.
的最小值为__________.
参考答案:
【答案】1
【解析】由ln(b+1)+a3b=0,得a=3bln(b+1),则点(b,a)是曲线y=3xln(x+1)上的任意一点,
由2dc![]() =0,得c=2d
=0,得c=2d![]() ,则点(d,c)是直线y=2x
,则点(d,c)是直线y=2x![]() 上的任意一点,
上的任意一点,
因为(ac)2+(bd)2表示点(b,a)到点(d,c)的距离的平方,即曲线上的一点与直线上一点的距离的平方,
所以(ac)2+(bd)2的最小值就是曲线上的点到直线距离的最小值的平方,即曲线上与直线y=2x![]() 平行的切线到该直线的距离的平方。
平行的切线到该直线的距离的平方。
![]() ,令y′=2,得x=0,此时y=0,即过原点的切线方程为y=2x,
,令y′=2,得x=0,此时y=0,即过原点的切线方程为y=2x,
则曲线上的点到直线距离的最小值的平方d2=![]() =1.
=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】社会调查人员希望从对人群的随机抽样调查中得到对他们所提问题诚实的回答,但是被采访者常常不愿意如实做出应答.
1965年Stanley·L.Warner发明了一种应用概率知识来消除这种不愿意情绪的方法.Warner的随机化应答方法要求人们随机地回答所提问题中的一个,而不必告诉采访者回答的是哪个问题,两个问题中有一个是敏感的或者是令人为难的,另一个是无关紧要的,这样应答者将乐意如实地回答问题,因为只有他知道自己回答的是哪个问题.
假如在调查运动员服用兴奋剂情况的时候,无关紧要的问题是:你的身份证号码的尾数是奇数吗;敏感的问题是:你服用过兴奋剂吗.然后要求被调查的运动员掷一枚硬币,如果出现正面,就回答第一个问题,否则回答第二个问题.
例如我们把这个方法用于200个被调查的运动员,得到56个“是”的回答,请你估计这群运动员中大约有百分之几的人服用过兴奋剂.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某志愿者到某山区小学支教,为了解留守儿童的幸福感,该志愿者对某班40名学生进行了一次幸福指数的调查问卷,并用茎叶图表示如下(注:图中幸福指数低于70,说明孩子幸福感弱;幸福指数不低于70,说明孩子幸福感强).
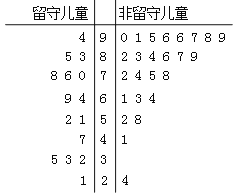
(Ⅰ)根据茎叶图中的数据完成
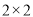 列联表,并判断能否有
列联表,并判断能否有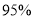 的把握认为孩子的幸福感强与是否是留守儿童有关?
的把握认为孩子的幸福感强与是否是留守儿童有关? 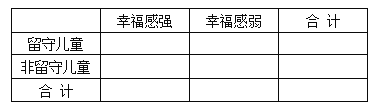
(Ⅱ)从15个留守儿童中按幸福感强弱进行分层抽样,共抽取5人,又在这5人中随机抽取2人进行家访,求这2个学生中恰有一人幸福感强的概率.
参考公式:
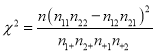 ; 附表:
; 附表: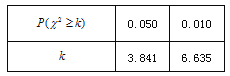
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x-
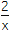 +a(2-ln x)(a>0),求函数f(x)的单调区间与极值点.
+a(2-ln x)(a>0),求函数f(x)的单调区间与极值点. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
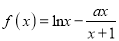 .
.(Ⅰ)若函数
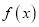 有极值,求实数
有极值,求实数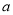 的取值范围;
的取值范围; (Ⅱ)当
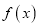 有两个极值点(记为
有两个极值点(记为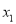 和
和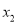 )时,求证:
)时,求证: 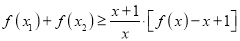 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
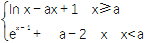 .(a>0)
.(a>0)(1)若a=1,证明:y=f(x)在R上单调递减;
(2)当a>1时,讨论f(x)零点的个数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产电饭煲,每年需投入固定成本40万元,每生产1万件还需另投入16万元的变动成本,设该公司一年内共生产电饭煲
 万件并全部销售完,每一万件的销售收入为
万件并全部销售完,每一万件的销售收入为 万元,且
万元,且 (
( ),该公司在电饭煲的生产中所获年利润为
),该公司在电饭煲的生产中所获年利润为 (万元),(注:利润=销售收入-成本)
(万元),(注:利润=销售收入-成本)(1)写出年利润
 (万元)关于年产量
(万元)关于年产量 (万件)的函数解析式,并求年利润的最大值;
(万件)的函数解析式,并求年利润的最大值;(2)为了让年利润
 不低于2360万元,求年产量
不低于2360万元,求年产量 的取值范围.
的取值范围.
相关试题

