【题目】有两个不透明的箱子,每个箱子都装有4个完全相同的小球,球上分别标有数字1,2,3,4.
(1)甲从其中一个箱子中摸出一个球,乙从另一个箱子摸出一个球,谁摸出的球上标的数字大谁就获胜(若数字相同则为平局),求甲获胜的概率;
(2)摸球方法与(1)同,若规定:两人摸到的球上所标数字相同甲获胜,所标数字不相同则乙获胜,这样规定公平吗?请说明理由。
参考答案:
【答案】解:(Ⅰ)用![]() (
(![]() 表示甲摸到的数字,
表示甲摸到的数字,![]() 表示乙摸到的数字)表示甲、乙各
表示乙摸到的数字)表示甲、乙各
摸一球构成的基本事件,则基本事件有:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、
![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共16个;3分
,共16个;3分
设:甲获胜的的事件为A,则事件A包含的基本事件有:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共有6个;则
,共有6个;则![]() …………………………6分
…………………………6分
(Ⅱ)设:甲获胜的的事件为B,乙获胜的的事件为C;事件B所包含的基本事件有:![]() 、
、![]() 、
、![]() 、
、![]() ,共有4个;则
,共有4个;则![]()
![]() …………………………10分
…………………………10分
![]() ,所以这样规定不公平. …………………11分
,所以这样规定不公平. …………………11分
答:(Ⅰ)甲获胜的概率为![]() ;(Ⅱ)这样规定不公平. ………… 12分
;(Ⅱ)这样规定不公平. ………… 12分
【解析】略
-
科目: 来源: 题型:
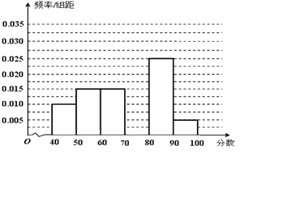
查看答案和解析>>【题目】某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60), ...,[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ) 从成绩在[40,50)和[90,100]的学生中任选两人,求他们在同一分数段的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的三棱锥
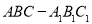 中,
中,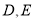 分别是
分别是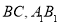 的中点.
的中点.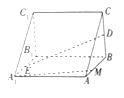
(1)求证:
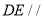 平面
平面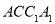 ;
;(2)若
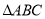 为正三角形,且
为正三角形,且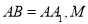 为
为 上的一点,
上的一点,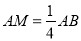 ,求直线
,求直线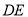 与直线
与直线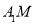 所成角的正切值.
所成角的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
 中,已知曲线
中,已知曲线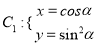 (
(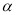 为参数),在以
为参数),在以 为极点,
为极点,  轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线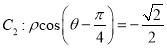 ,曲线
,曲线 .
.(1)求曲线
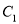 与
与 的交点
的交点 的直角坐标;
的直角坐标;(2)设点
 ,
,  分别为曲线
分别为曲线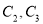 上的动点,求
上的动点,求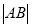 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
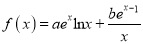 ,曲线y=f(x)在点(1, f(1))处的切线方程为y=e(x-1)+2.
,曲线y=f(x)在点(1, f(1))处的切线方程为y=e(x-1)+2.(1)求
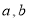 (2)证明:
(2)证明: 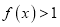
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
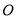 为坐标原点,对于函数
为坐标原点,对于函数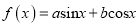 ,称向量
,称向量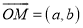 为函数
为函数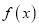 的伴随向量,同时称函数
的伴随向量,同时称函数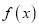 为向量
为向量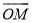 的伴随函数.
的伴随函数. (Ⅰ)设函数
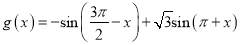 ,试求
,试求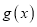 的伴随向量
的伴随向量 ;
; (Ⅱ)记向量
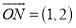 的伴随函数为
的伴随函数为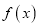 ,求当
,求当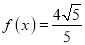 且
且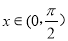 时
时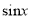 的值;
的值;(Ⅲ)由(Ⅰ)中函数
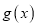 的图像(纵坐标不变)横坐标伸长为原来的
的图像(纵坐标不变)横坐标伸长为原来的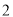 倍,再把整个图像向右平移
倍,再把整个图像向右平移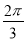 个单位长度得到
个单位长度得到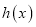 的图像。已知
的图像。已知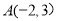
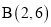 ,问在
,问在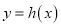 的图像上是否存在一点
的图像上是否存在一点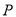 ,使得
,使得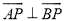 .若存在,求出
.若存在,求出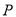 点坐标;若不存在,说明理由。
点坐标;若不存在,说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响,已知某学生只选修甲的概率为0.08,只选修甲和乙的概率是0.12,至少选修一门的概率是0.88,用
 表示该学生选修的课程门数和没有选修的课程门数的乘积.
表示该学生选修的课程门数和没有选修的课程门数的乘积.(1)记“函数
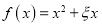 为
为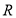 上的偶函数”为事件
上的偶函数”为事件 ,求事件
,求事件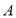 的概率;
的概率;(2)求
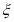 的分布列和数学期望.
的分布列和数学期望.
相关试题

