【题目】某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响,已知某学生只选修甲的概率为0.08,只选修甲和乙的概率是0.12,至少选修一门的概率是0.88,用![]() 表示该学生选修的课程门数和没有选修的课程门数的乘积.
表示该学生选修的课程门数和没有选修的课程门数的乘积.
(1)记“函数![]() 为
为![]() 上的偶函数”为事件
上的偶函数”为事件![]() ,求事件
,求事件![]() 的概率;
的概率;
(2)求![]() 的分布列和数学期望.
的分布列和数学期望.
参考答案:
【答案】(1)![]() ;(2)分布列见解析,
;(2)分布列见解析,![]() .
.
【解析】
试题分析:(1)由于学生是否选修哪门课互不影响,利用相互独立事件同时发生的概率解出学生选修甲、乙、丙的概率,由题意得到![]() 时,表示该学生选修三门功课或三门功课都没选,根据互斥事件的概率公
时,表示该学生选修三门功课或三门功课都没选,根据互斥事件的概率公
式得到结果;(2)用![]() 表示该学生选修的课程门数和没有选修的课程门数的乘积,所以变量的取值是
表示该学生选修的课程门数和没有选修的课程门数的乘积,所以变量的取值是![]() 或
或![]() ,结合第一问解出概率,写出分布列,算出期望.
,结合第一问解出概率,写出分布列,算出期望.
试题解析:该学生选修甲、乙、丙的概率分别为![]() ,
,
依题意得 ,解得
,解得 .
.
(1)若函数![]() 为
为![]() 上的偶函数,则
上的偶函数,则![]() .
.
当![]() 时,表示该学生选修三门功课或三门功课都没选,
时,表示该学生选修三门功课或三门功课都没选,
∴![]()
![]() ,
,
∴事件![]() 的概率为
的概率为![]() .
.
(2)依题意知![]() .
.
则![]() 的分布列为
的分布列为
| 0 | 2 |
| 0.24 | 0.76 |
∴![]() 的数学期望为
的数学期望为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有两个不透明的箱子,每个箱子都装有4个完全相同的小球,球上分别标有数字1,2,3,4.
(1)甲从其中一个箱子中摸出一个球,乙从另一个箱子摸出一个球,谁摸出的球上标的数字大谁就获胜(若数字相同则为平局),求甲获胜的概率;
(2)摸球方法与(1)同,若规定:两人摸到的球上所标数字相同甲获胜,所标数字不相同则乙获胜,这样规定公平吗?请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
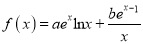 ,曲线y=f(x)在点(1, f(1))处的切线方程为y=e(x-1)+2.
,曲线y=f(x)在点(1, f(1))处的切线方程为y=e(x-1)+2.(1)求
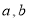 (2)证明:
(2)证明: 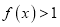
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 为坐标原点,对于函数
为坐标原点,对于函数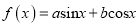 ,称向量
,称向量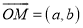 为函数
为函数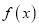 的伴随向量,同时称函数
的伴随向量,同时称函数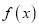 为向量
为向量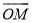 的伴随函数.
的伴随函数. (Ⅰ)设函数
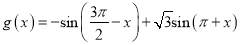 ,试求
,试求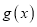 的伴随向量
的伴随向量 ;
; (Ⅱ)记向量
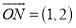 的伴随函数为
的伴随函数为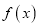 ,求当
,求当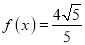 且
且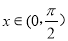 时
时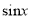 的值;
的值;(Ⅲ)由(Ⅰ)中函数
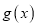 的图像(纵坐标不变)横坐标伸长为原来的
的图像(纵坐标不变)横坐标伸长为原来的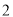 倍,再把整个图像向右平移
倍,再把整个图像向右平移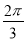 个单位长度得到
个单位长度得到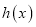 的图像。已知
的图像。已知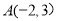
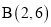 ,问在
,问在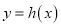 的图像上是否存在一点
的图像上是否存在一点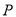 ,使得
,使得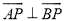 .若存在,求出
.若存在,求出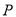 点坐标;若不存在,说明理由。
点坐标;若不存在,说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】平潭国际“花式风筝冲浪”集训队,在平潭龙凤头海滨浴场进行集训,海滨区域的某个观测点观测到该处水深
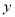 (米)是随着一天的时间
(米)是随着一天的时间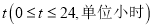 呈周期性变化,某天各时刻
呈周期性变化,某天各时刻 的水深数据的近似值如下表:
的水深数据的近似值如下表: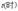
0
3
6
9
12
15
18
21
24
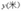
1.5
2.4
1.5
0.6
1.4
2.4
1.6
0.6
1.5
(Ⅰ)根据表中近似数据画出散点图(坐标系在答题卷中).观察散点图,从
①
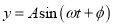 , ②
, ②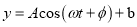 ,③
,③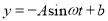
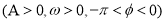 中选择一个合适的函数模型,并求出该拟合模型的函数解析式;(Ⅱ)为保证队员安全,规定在一天中的5~18时且水深不低于1.05米的时候进行训练,根据(Ⅰ) 中的选择的函数解析式,试问:这一天可以安排什么时间段组织训练,才能确保集训队员的安全。
中选择一个合适的函数模型,并求出该拟合模型的函数解析式;(Ⅱ)为保证队员安全,规定在一天中的5~18时且水深不低于1.05米的时候进行训练,根据(Ⅰ) 中的选择的函数解析式,试问:这一天可以安排什么时间段组织训练,才能确保集训队员的安全。 -
科目: 来源: 题型:
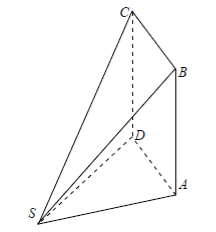
查看答案和解析>>【题目】如图,多面体
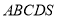 中,面
中,面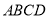 为矩形,
为矩形,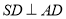 ,且
,且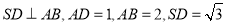 .
.
(1)求证:
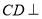 平面
平面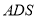 ;
;(2)求
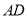 与
与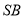 所成角的余弦值;
所成角的余弦值;(3)求二面角
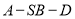 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数h(x)=(m2-5m+1)xm+1为幂函数,且为奇函数.
(I)求m的值;
(II)求函数g(x)=h(x)+
 ,x∈
,x∈ 的值域.
的值域.
相关试题

