【题目】已知直三棱柱ABC﹣A1B1C1的底面为正三角形,E,F分别是A1C1 , B1C1上的点,且满足A1E=EC1 , B1F=3FC1 . 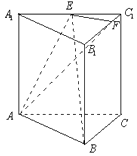
(1)求证:平面AEF⊥平面BB1C1C;
(2)设直三棱柱ABC﹣A1B1C1的棱长均相等,求二面角C1﹣AE﹣B的余弦值.
参考答案:
【答案】
(1)证明:取B1C1的中点G,连结A1G,
∵B1F=3FC1,FG=FC1,∴EF∥A1G,
在等边△A1B1C1中,由G是B1C1的中点,知A1G⊥B1C1,
∴EF⊥B1C1,
∵三棱柱ABC﹣A1B1C1是直棱柱,∴BB1⊥平面A1B1C1,
又∵EF平面A1B1C1,∴BB1⊥EF,
∵BB1∩B1C1=B1,∴EF⊥平面BB1C1C,
又EF平面AEF,∴平面AEF⊥平面BB1C1C
(2)解:以A为坐标原点,以AA1,AC分别为y轴,z轴,建立空间直角坐标系,
设直三棱柱ABC﹣A1B1C1的棱均为2,则A(0,0,0),B( ![]() ),E(0,1,2),
),E(0,1,2),
∴ ![]() =(0,1,2),
=(0,1,2), ![]() =(
=( ![]() ),
),
设 ![]() =(x,y,z)是平面ABE的一个法向量,
=(x,y,z)是平面ABE的一个法向量,
由 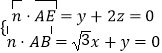 ,取x=﹣2,得
,取x=﹣2,得 ![]() =(﹣2,2
=(﹣2,2 ![]() ,﹣
,﹣ ![]() ),
),
平面AEC1的一个法向量 ![]() =(1,0,0),
=(1,0,0),
设二面角C1﹣AE﹣B的平面角为θ,
则cosθ= ![]() =
= ![]() .
.
∴二面角C1﹣AE﹣B的余弦值为 ![]() .
.
【解析】(1)取B1C1的中点G,连结A1G,推导出EF∥A1G,A1G⊥B1C1 , 从而EF⊥B1C1 , 由三棱柱ABC﹣A1B1C1是直棱柱,得到BB1⊥EF,从而EF⊥平面BB1C1C,由此能证明平面AEF⊥平面BB1C1C.(2)以A为坐标原点,以AA1 , AC分别为y轴,z轴,建立空间直角坐标系,利用向量法能求出二面角C1﹣AE﹣B的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知锐角三角形ABC中,角A,B,C所对的边分别为a,b,c若c﹣a=2acosB,则
 的取值范围是 .
的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}中,a1=1,a3=9,且an=an﹣1+λn﹣1(n≥2).
( I)求λ的值及数列{an}的通项公式;
( II)设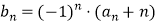 ,且数列{bn}的前n项和为Sn , 求S2n .
,且数列{bn}的前n项和为Sn , 求S2n . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的左、右焦点分别为F1(-c,0),F2(c,0),直线
的左、右焦点分别为F1(-c,0),F2(c,0),直线 交椭圆E于A,B两点,△ABF1的周长为16,△AF1F2的周长为12.
交椭圆E于A,B两点,△ABF1的周长为16,△AF1F2的周长为12.(1)求椭圆E的标准方程与离心率;
(2)若直线l与椭圆E交于C,D两点,且P(2,2)是线段CD的中点,求直线l的一般方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
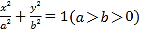 的右顶点为A,上顶点为B.已知椭圆的离心率为
的右顶点为A,上顶点为B.已知椭圆的离心率为 ,
, .
.(1)求椭圆的方程;
(2)设直线
 与椭圆交于
与椭圆交于 ,
, 两点,
两点, 与直线
与直线 交于点M,且点P,M均在第四象限.若
交于点M,且点P,M均在第四象限.若 的面积是
的面积是 面积的2倍,求
面积的2倍,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了解老人们的健康状况,政府从 老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能 自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行 统计,样本分布被制作成如图表:
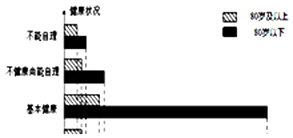
(1)若采取分层抽样的方法再从样本中的不能自理的老人中抽取16人进一步了解他们的生活状况,则两个群体中各应抽取多少人?
(2)估算该市80岁及以上长者占全市户籍人口的百分比;
(3)据统计该市大约有五分之一的户籍老人无固定收入,政府计划为这部分老人每月发 放生活补贴,标准如下:①80岁及以上长者每人每月发放生活补贴200元;②80岁以下 老人每人每月发放生活补贴120元;③不能自理的老人每人每月额外发放生活补贴100 元.试估计政府执行此计划的年度预算. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知中心在原点的双曲线
 的右焦点为
的右焦点为 ,右顶点为
,右顶点为 .
.(1)求双曲线
 的方程;
的方程;(2)若直线
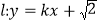 与双曲线
与双曲线 恒有两个不同的交点
恒有两个不同的交点 和
和 ,且
,且 (其中
(其中 为坐标原点),求实数
为坐标原点),求实数 取值范围.
取值范围.
相关试题

