【题目】矩形![]() 的两条对角线相交于点
的两条对角线相交于点![]() ,
, ![]() 边所在的直线的方程为
边所在的直线的方程为![]() ,点
,点![]() 在边
在边![]() 所在的直线上.
所在的直线上.
(1)求边![]() 所在直线的方程;
所在直线的方程;
(2)求矩形![]() 外接圆的方程;
外接圆的方程;
(3)过点![]() 的直线
的直线![]() 被矩形
被矩形![]() 的外接圆截得的弦长为
的外接圆截得的弦长为![]() ,求直线
,求直线![]() 的方程.
的方程.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)根据垂直关系,由直线![]() 的方程可得直线AD的斜率,然后由点斜式求直线方程即可;(2)由直线AB,AD的方程可求得点A的坐标,即圆心坐标,从而可得半径
的方程可得直线AD的斜率,然后由点斜式求直线方程即可;(2)由直线AB,AD的方程可求得点A的坐标,即圆心坐标,从而可得半径![]() ,可求得圆的标准方程;(3)分直线
,可求得圆的标准方程;(3)分直线![]() 的的斜率存在和不存在两种情况,利用待定系数法求解,根据圆的弦长公式求解。
的的斜率存在和不存在两种情况,利用待定系数法求解,根据圆的弦长公式求解。
试题解析:
(1)∵![]() ,
,
![]() ,
,
又点![]() 在边
在边![]() 所在的直线上,
所在的直线上,
∴边![]() 所在直线的方程为
所在直线的方程为![]() ,
,
即![]() .
.
(2)由![]() ,解得
,解得![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
∵矩形![]() 的两条对角线相交于点
的两条对角线相交于点![]() ,即圆心为
,即圆心为![]() ,
,
∴![]() ,
,
∴矩形![]() 外接圆的方程
外接圆的方程![]() .
.
(3)①当直线斜率不存在时,
直线方程为![]() ,与圆的交点为
,与圆的交点为![]() 和
和![]() ,
,
∴弦长为![]() 。
。
②当直线斜率存在时,
设直线为![]() ,即
,即![]() ,
,
由题意得圆心到直线的距离为1,
∴![]() ,解得
,解得![]() ,
,
∴直线为![]() ,
,
综上直线![]() 的方程为
的方程为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂拟造一座平面为长方形,面积为
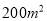 的三级污水处理池.由于地形限制,长、宽都不能超过
的三级污水处理池.由于地形限制,长、宽都不能超过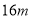 ,处理池的高度一定.如果池的四周墙壁的造价为
,处理池的高度一定.如果池的四周墙壁的造价为 元
元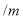 ,中间两道隔墙的造价为
,中间两道隔墙的造价为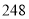 元
元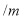 ,池底的造价为
,池底的造价为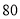 元
元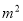 ,则水池的长、宽分別为多少米时,污水池的造价最低?最低造价为多少元?
,则水池的长、宽分別为多少米时,污水池的造价最低?最低造价为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
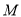 :
: 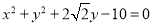 和点
和点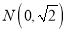 ,动圆
,动圆 经过点
经过点 且与圆
且与圆 相切,圆心
相切,圆心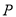 的轨迹为曲线
的轨迹为曲线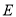 .
.(1)求曲线
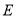 的方程;
的方程;(2)点
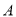 是曲线
是曲线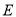 与
与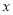 轴正半轴的交点,点
轴正半轴的交点,点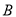 ,
, 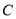 在曲线
在曲线 上,若直线
上,若直线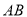 ,
, 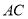 的斜率分别是
的斜率分别是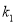 ,
, 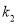 ,满足
,满足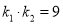 ,求
,求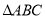 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
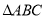 的顶点
的顶点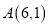 ,
, 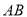 边上的中线
边上的中线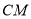 所在直线方程为
所在直线方程为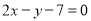 ,
,  边上的高
边上的高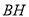 所在直线方程为
所在直线方程为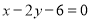 .
. (1)求点
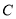 的坐标;
的坐标;(2)求直线
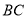 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
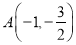 是椭圆
是椭圆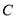 :
: 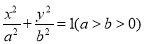 上的一点,椭圆的右焦点为
上的一点,椭圆的右焦点为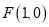 ,斜率为
,斜率为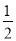 的直线
的直线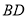 交椭圆
交椭圆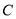 于
于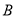 、
、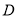 两点,且
两点,且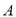 、
、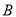 、
、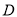 三点互不重合.
三点互不重合.(1)求椭圆
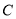 的方程;
的方程;(2)求证:直线
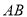 ,
, 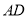 的斜率之和为定值.
的斜率之和为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
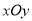 中,二次函数
中,二次函数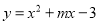 的图象与
的图象与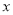 轴交于
轴交于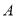 ,
, 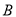 两点,点
两点,点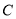 的坐标为
的坐标为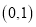 .当
.当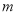 变化时,解答下列问题:
变化时,解答下列问题:(1)以
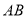 为直径的圆能否经过点
为直径的圆能否经过点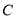 ?说明理由;
?说明理由;(2)过
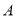 ,
, 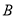 ,
, 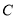 三点的圆在
三点的圆在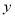 轴上截得的弦长是否为定值?若是,则求出该定值;若不是,请说明理由.
轴上截得的弦长是否为定值?若是,则求出该定值;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
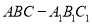 中,侧棱
中,侧棱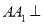 平面
平面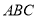 ,
, 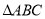 为等腰直角三角形,
为等腰直角三角形, 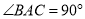 ,
,  ,
,  分别是
分别是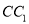 ,
, 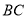 的中点,且
的中点,且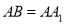 .
.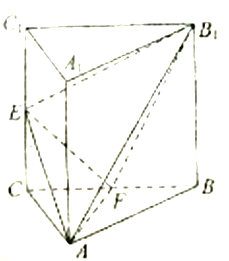
(Ⅰ)求证:
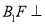 平面
平面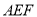 ;
;(Ⅱ)若
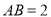 ,求点
,求点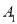 到平面
到平面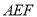 的距离 .
的距离 .
相关试题

