【题目】已知点![]() 是椭圆
是椭圆![]() :
: ![]() 上的一点,椭圆的右焦点为
上的一点,椭圆的右焦点为![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,且
两点,且![]() 、
、![]() 、
、![]() 三点互不重合.
三点互不重合.
(1)求椭圆![]() 的方程;
的方程;
(2)求证:直线![]() ,
, ![]() 的斜率之和为定值.
的斜率之和为定值.
参考答案:
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)由椭圆的定义可求得![]() ,然后可得
,然后可得![]() ,可得椭圆的方程;(2)设直线
,可得椭圆的方程;(2)设直线![]() 的方程为
的方程为![]() ,将此方程代入椭圆方程可得整理得
,将此方程代入椭圆方程可得整理得![]() ,设
,设![]() ,
, ![]() ,由根与系数的关系可得
,由根与系数的关系可得![]() ,
, ![]() ,然后由斜率公式可得
,然后由斜率公式可得![]() ,即可得到结论。
,即可得到结论。
试题解析:
(1)由题意得椭圆的左焦点为![]() 。
。
由椭圆定义可得
![]() ,
,
解得![]() ,
,
∴![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)证明:设直线![]() 的方程为
的方程为![]() ,
,
又![]() ,
, ![]() ,
, ![]() 三点不重合,故
三点不重合,故![]() 。
。
由 消去y整理得
消去y整理得![]() ,
,
∵直线与椭圆交于![]() 、
、![]() 两点,
两点,
∴![]() ,
,
解得![]()
设![]() ,
, ![]() ,
,
则![]() ,①
,① ![]() ,②
,②
设直线![]() ,
, ![]() 的斜率分别为
的斜率分别为![]() ,
, ![]() ,
,
则
![]() (
(![]() ),
),
分别将①②式代入(![]() ),得
),得
![]() ,
,
所以![]() ,
,
即直线![]() ,
, ![]() 的斜率之和为定值
的斜率之和为定值![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
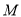 :
: 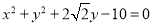 和点
和点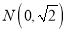 ,动圆
,动圆 经过点
经过点 且与圆
且与圆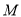 相切,圆心
相切,圆心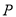 的轨迹为曲线
的轨迹为曲线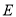 .
.(1)求曲线
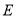 的方程;
的方程;(2)点
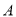 是曲线
是曲线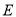 与
与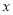 轴正半轴的交点,点
轴正半轴的交点,点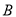 ,
, 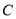 在曲线
在曲线 上,若直线
上,若直线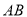 ,
, 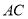 的斜率分别是
的斜率分别是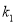 ,
, 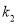 ,满足
,满足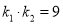 ,求
,求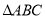 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
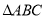 的顶点
的顶点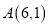 ,
, 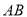 边上的中线
边上的中线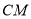 所在直线方程为
所在直线方程为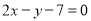 ,
,  边上的高
边上的高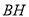 所在直线方程为
所在直线方程为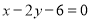 .
. (1)求点
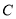 的坐标;
的坐标;(2)求直线
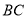 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】矩形
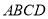 的两条对角线相交于点
的两条对角线相交于点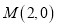 ,
, 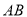 边所在的直线的方程为
边所在的直线的方程为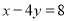 ,点
,点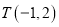 在边
在边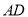 所在的直线上.
所在的直线上. (1)求边
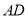 所在直线的方程;
所在直线的方程;(2)求矩形
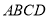 外接圆的方程;
外接圆的方程;(3)过点
 的直线
的直线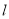 被矩形
被矩形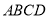 的外接圆截得的弦长为
的外接圆截得的弦长为 ,求直线
,求直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
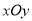 中,二次函数
中,二次函数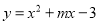 的图象与
的图象与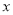 轴交于
轴交于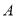 ,
, 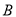 两点,点
两点,点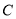 的坐标为
的坐标为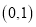 .当
.当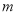 变化时,解答下列问题:
变化时,解答下列问题:(1)以
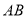 为直径的圆能否经过点
为直径的圆能否经过点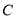 ?说明理由;
?说明理由;(2)过
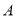 ,
, 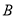 ,
, 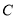 三点的圆在
三点的圆在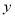 轴上截得的弦长是否为定值?若是,则求出该定值;若不是,请说明理由.
轴上截得的弦长是否为定值?若是,则求出该定值;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
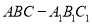 中,侧棱
中,侧棱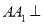 平面
平面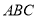 ,
, 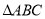 为等腰直角三角形,
为等腰直角三角形, 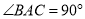 ,
, 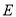 ,
, 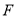 分别是
分别是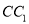 ,
, 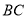 的中点,且
的中点,且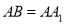 .
.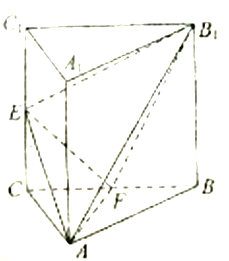
(Ⅰ)求证:
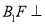 平面
平面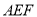 ;
;(Ⅱ)若
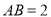 ,求点
,求点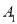 到平面
到平面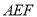 的距离 .
的距离 . -
科目: 来源: 题型:
查看答案和解析>>【题目】为选拔选手参加“中国谜语大会”,某中学举行了一次“谜语大赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为
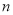 )进行统计.按照
)进行统计.按照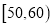 ,
, 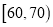 ,
, 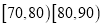 ,
, 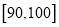 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在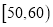 ,
, 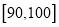 的数据).
的数据).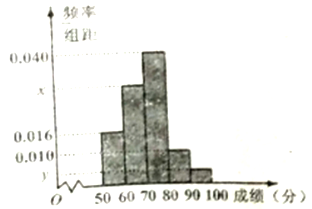

(Ⅰ)求样本容量
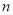 和频率分布直方图中的
和频率分布直方图中的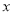 ,
, 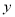 的值;
的值;(Ⅱ)分数在
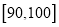 的学生设为一等奖,获奖学金500元;分数在
的学生设为一等奖,获奖学金500元;分数在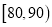 的学生设为二等奖,获奖学金200元.已知在样本中,获一、二等奖的学生中各有一名男生,则从剩下的女生中任取三人,求奖学金之和大于600的概率.
的学生设为二等奖,获奖学金200元.已知在样本中,获一、二等奖的学生中各有一名男生,则从剩下的女生中任取三人,求奖学金之和大于600的概率.
相关试题

