【题目】某工厂拟造一座平面为长方形,面积为![]() 的三级污水处理池.由于地形限制,长、宽都不能超过
的三级污水处理池.由于地形限制,长、宽都不能超过![]() ,处理池的高度一定.如果池的四周墙壁的造价为
,处理池的高度一定.如果池的四周墙壁的造价为![]() 元
元![]() ,中间两道隔墙的造价为
,中间两道隔墙的造价为![]() 元
元![]() ,池底的造价为
,池底的造价为![]() 元
元![]() ,则水池的长、宽分別为多少米时,污水池的造价最低?最低造价为多少元?
,则水池的长、宽分別为多少米时,污水池的造价最低?最低造价为多少元?
参考答案:
【答案】![]() ,
,![]() .
.
【解析】试题分析:应用问题首先要认真细致的审题,逐字逐句的读题,把实际问题转化为数学问题.首先根据提议设出未知数,根据各项造价表示出总造价建立函数模型,根据实际需要写出函数的定义域,由于![]() ,借助a,b关系进行减元,化为只含有a的函数关系,再利用均值不等式求最值.
,借助a,b关系进行减元,化为只含有a的函数关系,再利用均值不等式求最值.
试题解析:
设污水处理水池的长、宽分别为![]() ,总造价为y元,
,总造价为y元,
则![]() ,
,
![]()
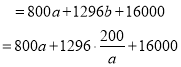 ,
, ![]()
易知函数是减函数,所以当![]() 时总造价最低,
时总造价最低,
最低造价为45000元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
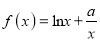 (
( ).
).(Ⅰ)若函数
 在
在 处的切线平行于直线
处的切线平行于直线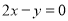 ,求实数
,求实数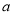 的值;
的值;(Ⅱ)讨论
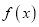 在
在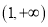 上的单调性;
上的单调性;(Ⅲ)若存在
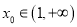 ,使得
,使得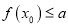 成立,求
成立,求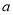 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)满足f(x)=x2﹣2(a+2)x+a2 , g(x)=﹣x2+2(a﹣2)x﹣a2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(max(p,q)表示p,q中的较大值,min(p,q)表示p,q中的较小值),记H1(x)的最小值为A,H2(x)的最大值为B,则A﹣B=( )
A.a2﹣2a﹣16
B.a2+2a﹣16
C.-16
D.16 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
,  分别为椭圆
分别为椭圆 :
:  的左、右焦点,点
的左、右焦点,点 在椭圆
在椭圆 上.
上.(Ⅰ)求
 的最小值;
的最小值;(Ⅱ)设直线
 的斜率为
的斜率为 ,直线
,直线 与椭圆
与椭圆 交于
交于 ,
,  两点,若点
两点,若点 在第一象限,且
在第一象限,且 ,求
,求 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
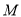 :
: 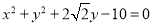 和点
和点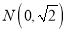 ,动圆
,动圆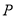 经过点
经过点 且与圆
且与圆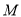 相切,圆心
相切,圆心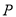 的轨迹为曲线
的轨迹为曲线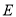 .
.(1)求曲线
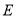 的方程;
的方程;(2)点
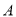 是曲线
是曲线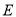 与
与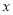 轴正半轴的交点,点
轴正半轴的交点,点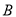 ,
, 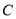 在曲线
在曲线 上,若直线
上,若直线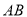 ,
, 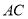 的斜率分别是
的斜率分别是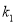 ,
, 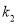 ,满足
,满足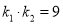 ,求
,求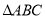 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
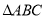 的顶点
的顶点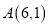 ,
, 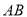 边上的中线
边上的中线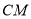 所在直线方程为
所在直线方程为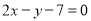 ,
,  边上的高
边上的高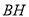 所在直线方程为
所在直线方程为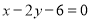 .
. (1)求点
 的坐标;
的坐标;(2)求直线
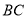 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】矩形
 的两条对角线相交于点
的两条对角线相交于点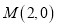 ,
, 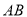 边所在的直线的方程为
边所在的直线的方程为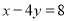 ,点
,点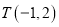 在边
在边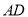 所在的直线上.
所在的直线上. (1)求边
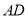 所在直线的方程;
所在直线的方程;(2)求矩形
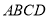 外接圆的方程;
外接圆的方程;(3)过点
 的直线
的直线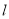 被矩形
被矩形 的外接圆截得的弦长为
的外接圆截得的弦长为 ,求直线
,求直线 的方程.
的方程.
相关试题

