【题目】设函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)求证:当![]() 时,
时, ![]() .
.
参考答案:
【答案】(1)![]() 的单调递减区间为
的单调递减区间为![]() ;
; ![]() 的单调递增区间为
的单调递增区间为![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】【试题分析】(1)直接对函数![]() 求导得
求导得![]() ,借助导函数值的符号与函数单调性之间的关系求出其单调区间;(2)先将不等式
,借助导函数值的符号与函数单调性之间的关系求出其单调区间;(2)先将不等式![]() 中参数分离分离出来可得:
中参数分离分离出来可得: ![]() ,再构造函数
,再构造函数![]() ,
, ![]() ,求导得
,求导得![]() ,借助
,借助![]() ,推得
,推得![]() ,从而
,从而![]() 在
在![]() 上单调递减,
上单调递减, ![]() ,进而求得
,进而求得![]() ;(3)先将不等式
;(3)先将不等式![]() 等价转化为
等价转化为![]() ,再构造函数
,再构造函数![]() ,求导可得
,求导可得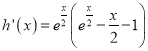 ,由(2)知
,由(2)知![]() 时,
时, ![]() 恒成立,所以
恒成立,所以![]() ,即
,即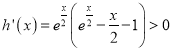 恒成立,故
恒成立,故![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,因此
,因此![]() 时,有
时,有![]() :
:
解:(1))当![]() 时,则
时,则![]() ,令
,令![]() 得
得![]() ,所以有
,所以有
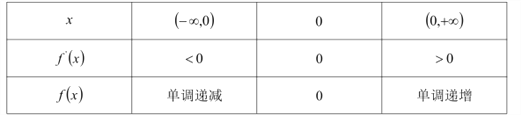
即![]() 时,
时, ![]() 的单调递减区间为
的单调递减区间为![]() ;
; ![]() 的单调递增区间为
的单调递增区间为![]() .
.
(2)由![]() ,分离参数可得:
,分离参数可得: ![]() ,
,
设![]() ,
, ![]() ,
,
∴![]() ,又∵
,又∵![]() ,
,
∴![]() ,则
,则![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,∴
,∴![]()
即![]() 的取值范围为
的取值范围为![]() .
.
(3)证明: ![]() 等价于
等价于![]()
设![]() ,
,
∴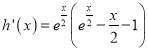 ,由(2)知
,由(2)知![]() 时,
时, ![]() 恒成立,
恒成立,
所以![]() ,
,
∴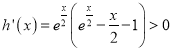 恒成立
恒成立
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,因此
,因此![]() 时,有
时,有![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 已知函数
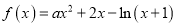 (a为常数).
(a为常数).(Ⅰ)当
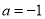 时,求函数
时,求函数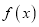 的单调区间;
的单调区间;(Ⅱ)当
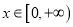 时,不等式
时,不等式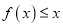 恒成立,求实数
恒成立,求实数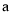 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正四面体
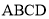 的棱长为
的棱长为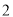 ,
, 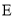 为棱
为棱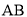 的中点,过
的中点,过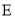 作其外接球的截面,则截面面积的最小值为__________.
作其外接球的截面,则截面面积的最小值为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】解答
(1)已知f(x)= ,证明:f(x)是R上的增函数;
,证明:f(x)是R上的增函数;
(2)解方程:log5(3﹣25x)=2x. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)=2x2﹣4x.
(1)指出图象的开口方向、对称轴方程、顶点坐标;
(2)用描点法画出它的图象;
(3)求出函数的最值,并分析函数的单调性. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
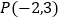 是函数
是函数 图象上的点,
图象上的点,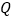 是双曲线在第四象限这一分支上的动点,过点
是双曲线在第四象限这一分支上的动点,过点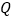 作直线,使其与双曲线
作直线,使其与双曲线 只有一个公共点,且与
只有一个公共点,且与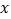 轴、
轴、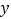 轴分别交于点
轴分别交于点 、
、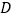 ,另一条直线
,另一条直线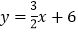 与
与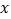 轴、
轴、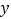 轴分别交于点
轴分别交于点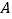 、
、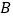 .
.则(1)
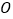 为坐标原点,三角形
为坐标原点,三角形 的面积为__________.
的面积为__________.(2)四边形
 面积的最小值为__________.
面积的最小值为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).

(1)分别写出两种产品的收益与投资额的函数关系式;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
相关试题

