【题目】解答
(1)已知f(x)= ![]() ,证明:f(x)是R上的增函数;
,证明:f(x)是R上的增函数;
(2)解方程:log5(3﹣25x)=2x.
参考答案:
【答案】
(1)
证明:证法一:
设x1<x2,则 ![]()
∴f(x1)﹣f(x2)= ![]() ﹣
﹣ ![]() =
= ![]() <0,
<0,
∴f(x1)<f(x2),
∴f(x)是R上的增函数.
证法二:f(x)= ![]() =1﹣
=1﹣ ![]() ,
,
∴f′(x)= ![]() ,
,
∵f′(x)>0恒成立,
故f(x)是R上的增函数
(2)
解:由解得原方程可得3﹣25x=52x,
整理得(5x﹣1)(5x+3)=0,
∵5x+3>3≠0,
∴5x﹣1=0,
解得x=0,
∴所求方程的解集为{0}
【解析】(1)证法一:设x1<x2 , 作差判断出f(x1)<f(x2),根据函数单调性的定义,可得:f(x)是R上的增函数.证法二:求导,根据f′(x)>0恒成立,可得:f(x)是R上的增函数.(2)原方程可化为3﹣25x=52x , 即(5x﹣1)(5x+3)=0,由5x+3>3≠0得:5x﹣1=0,解得答案.
【考点精析】本题主要考查了函数单调性的判断方法和利用导数研究函数的单调性的相关知识点,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形
 中,
中, 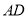 //
// 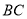 ,
, 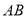 ⊥
⊥ ,
, 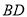 ⊥
⊥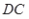 , 点
, 点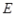 是
是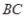 边的中点, 将△
边的中点, 将△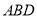 沿
沿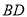 折起,使平面
折起,使平面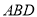 ⊥平面
⊥平面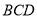 ,连接
,连接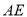 ,
, 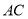 ,
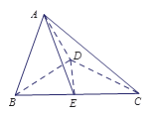
, 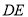 , 得到如
, 得到如图所示的空间几何体.
(Ⅰ)求证:
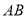 ⊥平面
⊥平面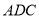 ;
;(Ⅱ)若
 ,求点
,求点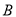 到平面
到平面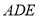 的距离.
的距离.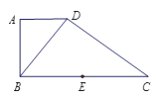
-
科目: 来源: 题型:
查看答案和解析>>【题目】 已知函数
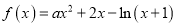 (a为常数).
(a为常数).(Ⅰ)当
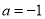 时,求函数
时,求函数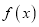 的单调区间;
的单调区间;(Ⅱ)当
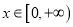 时,不等式
时,不等式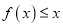 恒成立,求实数
恒成立,求实数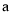 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正四面体
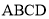 的棱长为
的棱长为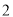 ,
, 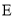 为棱
为棱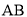 的中点,过
的中点,过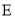 作其外接球的截面,则截面面积的最小值为__________.
作其外接球的截面,则截面面积的最小值为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
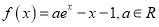 .
.(1)当
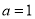 时,求
时,求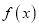 的单调区间;
的单调区间;(2)当
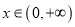 时,
时, 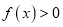 恒成立,求
恒成立,求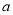 的取值范围;
的取值范围;(3)求证:当
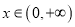 时,
时, 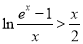 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)=2x2﹣4x.
(1)指出图象的开口方向、对称轴方程、顶点坐标;
(2)用描点法画出它的图象;
(3)求出函数的最值,并分析函数的单调性. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
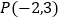 是函数
是函数 图象上的点,
图象上的点,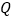 是双曲线在第四象限这一分支上的动点,过点
是双曲线在第四象限这一分支上的动点,过点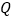 作直线,使其与双曲线
作直线,使其与双曲线 只有一个公共点,且与
只有一个公共点,且与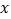 轴、
轴、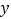 轴分别交于点
轴分别交于点 、
、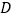 ,另一条直线
,另一条直线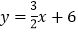 与
与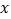 轴、
轴、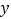 轴分别交于点
轴分别交于点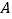 、
、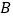 .
.则(1)
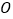 为坐标原点,三角形
为坐标原点,三角形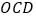 的面积为__________.
的面积为__________.(2)四边形
 面积的最小值为__________.
面积的最小值为__________.
相关试题

