【题目】已知函数![]() .
.
(1)已知![]() ,求
,求![]() 单调递增区间;
单调递增区间;
(2)是否存在实数![]() ,使
,使![]() 的最小值为0?若存在,求出
的最小值为0?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
参考答案:
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() .
.
【解析】
试题分析:(1)根据![]() 代入函数的解析式,解得
代入函数的解析式,解得![]() ,得到
,得到![]() ,求出函数的定义域,讨论真数对应的二次函数在函数定义域内的单调性,即可得到结论;(2)设存在实数
,求出函数的定义域,讨论真数对应的二次函数在函数定义域内的单调性,即可得到结论;(2)设存在实数![]() ,使
,使![]() 最小值为0,由于底数为
最小值为0,由于底数为![]() ,可得真数
,可得真数![]() 恒成立,在结合二次含的性质,列出不等式,即可求解结论.
恒成立,在结合二次含的性质,列出不等式,即可求解结论.
试题解析:∵![]() 且
且![]() ,
,
∴![]() ,∴
,∴![]() ,即
,即![]() ,
,
可得函数![]() ,
,
∵真数为![]() ,
,
∴函数的定义域为![]() ,
,
令![]() 可得,当
可得,当![]() 时,
时,![]() 为关于
为关于![]() 的增函数,
的增函数,
∵底数为![]() ,∴函数
,∴函数![]() 单调增区间为
单调增区间为![]() .
.
(2)设存在实数![]() ,使
,使![]() 最小值为0,由于底数为
最小值为0,由于底数为![]() ,可得真数
,可得真数![]() 恒成立,
恒成立,
且真数![]() 最小值恰好为1,即
最小值恰好为1,即![]() 为正数,且当
为正数,且当![]() 时,
时,![]() 值为1,
值为1,
所以 ∴
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有两个分类变量X与Y的一组数据,由其列联表计算得k≈4.523,则认为“X与Y有关系”犯错误的概率为( )
A. 95% B. 90% C. 5% D. 10%
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业生产的新产品必须先靠广告打开销路,该产品广告效应
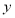 (单位:元)是产品的销售额与广告费
(单位:元)是产品的销售额与广告费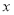 (单位:元)之间的差,如果销售额与广告费
(单位:元)之间的差,如果销售额与广告费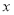 的算术平方根成正比,根据对市场的抽样调查,每付出100元的广告费,所得销售额是1000元.
的算术平方根成正比,根据对市场的抽样调查,每付出100元的广告费,所得销售额是1000元.(Ⅰ)求出广告效应
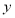 与广告费
与广告费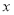 之间的函数关系式;
之间的函数关系式;(Ⅱ)该企业投入多少广告费才能获得最大的广告效应?是不是广告费投入越多越好?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面
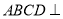 平面
平面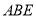 ,其中
,其中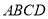 为矩形,
为矩形,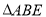 为直角三角形,
为直角三角形,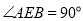 ,
,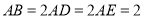 .
.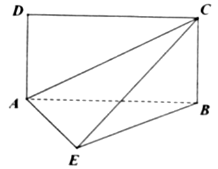
(1)求证:平面
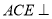 平面
平面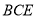 ;
;(2)求直线
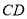 与平面
与平面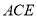 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
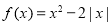 ,
, .
.(1)若方程
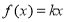 有三个解,试求实数
有三个解,试求实数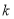 的取值范围;
的取值范围;(2)是否存在实数
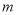 ,
,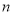 (
(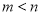 ),使函数
),使函数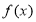 的定义域与值域均为
的定义域与值域均为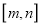 ?若存在,求出所有的区间
?若存在,求出所有的区间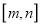 ,若不存在,说明理由.
,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四棱柱
 中,侧棱
中,侧棱 底面
底面 ,
, ,
, ,
, ,
, ,
, 为
为 的中点.
的中点.
(1)证明:
 ;
;(2)求二面角
 的正弦值;
的正弦值;(3)设点
 在线段
在线段 上,且直线
上,且直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,求线段
,求线段 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个几何体的三视图如图所示.

(1)求此几何体的表面积;
(2)如果点
 在正视图中所示位置:
在正视图中所示位置: 为所在线段中点,
为所在线段中点, 为顶点,求在几何体表面上,从
为顶点,求在几何体表面上,从 点到
点到 点的最短路径的长.
点的最短路径的长.
相关试题

