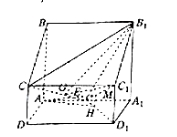
【题目】如图所示,四棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.

(1)证明:![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)设点![]() 在线段
在线段![]() 上,且直线
上,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长.
的长.
参考答案:
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)根据线面垂直有![]() ,计算得
,计算得![]() ,即
,即![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() ;(2)过
;(2)过![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() .由(1)知,
.由(1)知,![]() ,故
,故![]() 平面
平面![]() ,得
,得![]() .∴
.∴![]() 为二面角
为二面角![]() 的平面角.在
的平面角.在![]() 中计算得
中计算得![]() ;(3)连接
;(3)连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,可得
,可得![]() 平面
平面![]() ,连接
,连接![]() ,则
,则![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角.设
所成的角.设![]() ,在
,在![]() 中利用余弦定理建立关于
中利用余弦定理建立关于![]() 的方程,求得
的方程,求得![]() .
.
试题解析:
(1)∵侧棱![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() .
.
经计算可得![]() ,
,![]() ,
,![]() ,
,
∴![]() ,∴在
,∴在![]() 中,
中,![]() .
.
又∵![]() ,
,![]() 平面
平面![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() .又
.又![]() 平面
平面![]() ,
,
∴![]() .
.
(2)如图所示,过![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() .
.
由(1)知,![]() ,故
,故![]() 平面
平面![]() ,得
,得![]() .
.
∴![]() 为二面角
为二面角![]() 的平面角.
的平面角.
在![]() 中,由
中,由![]() ,
,![]() ,可得
,可得![]() .
.
在![]() 中,
中,![]() ,∴
,∴![]() ,
,
即二面角![]() 的正弦值为
的正弦值为![]() .
.
(3)如图所示,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,可得
,可得![]() 平面
平面![]() ,
,
连接![]() ,则
,则![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角.
所成的角.
设![]() ,从而在
,从而在![]() 中,有
中,有![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,![]() ,得
,得![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
由![]() ,
,
得![]() ,
,
整理得![]() ,解得
,解得![]() (负值舍去).
(负值舍去).
∴线段![]() 的长为
的长为![]() .
.
-
科目: 来源: 题型:
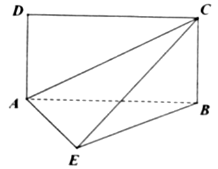
查看答案和解析>>【题目】如图,平面
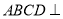 平面
平面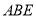 ,其中
,其中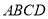 为矩形,
为矩形,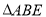 为直角三角形,
为直角三角形,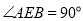 ,
,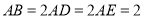 .
.
(1)求证:平面
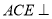 平面
平面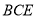 ;
;(2)求直线
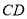 与平面
与平面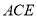 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
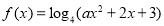 .
.(1)已知
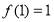 ,求
,求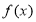 单调递增区间;
单调递增区间;(2)是否存在实数
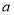 ,使
,使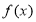 的最小值为0?若存在,求出
的最小值为0?若存在,求出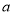 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
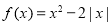 ,
, .
.(1)若方程
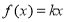 有三个解,试求实数
有三个解,试求实数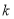 的取值范围;
的取值范围;(2)是否存在实数
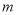 ,
,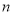 (
(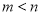 ),使函数
),使函数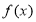 的定义域与值域均为
的定义域与值域均为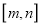 ?若存在,求出所有的区间
?若存在,求出所有的区间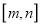 ,若不存在,说明理由.
,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个几何体的三视图如图所示.

(1)求此几何体的表面积;
(2)如果点
 在正视图中所示位置:
在正视图中所示位置: 为所在线段中点,
为所在线段中点, 为顶点,求在几何体表面上,从
为顶点,求在几何体表面上,从 点到
点到 点的最短路径的长.
点的最短路径的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点(-3,-1)和(4,-6)在直线3x-2y-a=0的两侧,则实数a的取值范围为( )
A. (-7,24)
B. (-∞,-7)∪(24,+∞)
C. (-24,7)
D. (-∞,-24)∪(7,+∞)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一项中学生近视情况的调查中,某校男生150名中有80名近视,女生140名中有70名近视,在检验这些中学生眼睛近视是否与性别有关时用什么方法最有说服力( )
A. 平均数与方差 B. 回归分析
C. 独立性检验 D. 概率
相关试题

