【题目】如图,在棱长均为4的三棱柱![]() 中,
中, ![]() 分别是
分别是![]() 和
和![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]()
(2)若平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
参考答案:
【答案】(1)证明见解析(2)8
【解析】试题分析:(1)欲证A1D1∥平面AB1D,根据直线与平面平行的判定定理可知只需证A1D1与平面AB1D内一直线平行,连接DD1,根据中位线定理可知B1D1∥BD,且B1D1=BD,则四边形B1BDD1为平行四边形,同理可证四边形AA1D1D为平行四边形,则A1D1∥AD
又A1D1平面AB1D,AD平面AB1D,满足定理所需条件;
(2)根据面面垂直的性质定理可知AD⊥平面B1C1CB,即AD是三棱锥A﹣B1BC的高,求出三棱锥A﹣B1BC的体积,从而求出三棱锥B1﹣ABC的体积.
试题解析:
(1)证明:如图,连结![]() .在三棱柱
.在三棱柱![]() 中,
中,
因为![]() 分别是
分别是![]() 与
与![]() 的中点,所以
的中点,所以![]() ,且
,且![]() .
.
所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,且
,且![]() .
.
又![]() 所以
所以![]() ,
,
所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() .
.
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() .
.

(2)解:(方法1)
在![]() 中,因为
中,因为![]() ,
, ![]() 为
为![]() 的中点,所以
的中点,所以![]() .
.
因为平面![]() 平面
平面![]() ,交线为
,交线为![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,即
,即![]() 是三棱锥
是三棱锥![]() 的高.
的高.
在![]() 中,由
中,由![]() ,得
,得![]() .
.
在![]() 中,
中, ![]() ,
,
所以![]() 的面积
的面积![]() .
.
所以三棱锥![]() 的体积,即三棱锥
的体积,即三棱锥![]() 的体积
的体积![]() .
.
(方法 2)在![]() 中,因为
中,因为![]() ,
,
所以![]() 为正三角形,因此
为正三角形,因此![]() .
.
因为平面![]() 平面
平面![]() ,交线为
,交线为![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,即
,即![]() 是三棱锥
是三棱锥![]() 的高.
的高.
在![]() 中,由
中,由![]() ,得
,得![]() 的面积
的面积![]() .
.
在![]() 中,因为
中,因为![]() ,所以
,所以![]() .
.
所以三棱锥![]() 的体积
的体积![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】祖暅是南北朝时代的伟大科学家,5世纪末提出体积计算原理,即祖暅原理:“幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现有以下四个几何体:图①是从圆柱中挖出一个圆锥所得的几何体;图②、图③、图④分别是圆锥、圆台和半球,则满足祖暅原理的两个几何体为( )
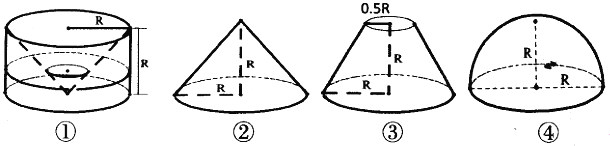
A. ①② B. ①③ C. ②④ D. ①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义域为
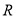 的函数
的函数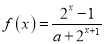 是奇函数.
是奇函数.(1)求
 的值;
的值; (2)证明:
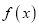 为
为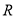 上的增函数;
上的增函数;(3)若对任意的
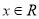 ,不等式
,不等式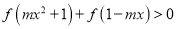 恒成立,求实数
恒成立,求实数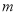 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业为了更好地了解设备改造前后与生产合格品的关系,随机抽取了180件产品进行分析,其中设备改造前的合格品有36件,不合格品有49件,设备改造后生产的合格品有65件,不合格品有30件.根据所给数据:
⑴写出
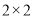 列联表;⑵判断产品是否合格与设备改造是否有关,说明理由.
列联表;⑵判断产品是否合格与设备改造是否有关,说明理由.附:
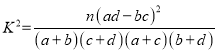 ,
, 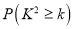
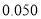
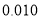
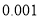
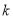
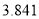
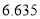
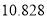
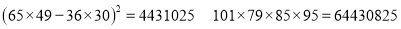
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分为14分)已知定义域为R的函数
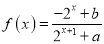 是奇函数.
是奇函数.(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】经销商经销某种农产品,在一个销售季度内,每售出
 该产品获利润500元,未售出的产品,每
该产品获利润500元,未售出的产品,每 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了
亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了 该农产品.以
该农产品.以 (
( )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量,  (单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:元)表示下一个销售季度内经销该农产品的利润.(Ⅰ)将
 表示为
表示为 的函数;
的函数;(Ⅱ)根据直方图估计利润
 不少于57000元的概率.
不少于57000元的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)用定义证明函数
 在
在 上是增函数;
上是增函数;(2)探究是否存在实数
 ,使得函数
,使得函数 为奇函数?若存在,求出
为奇函数?若存在,求出 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;(3)在(2)的条件下,解不等式
 .
.
相关试题

