【题目】已知定义域为![]() 的函数
的函数![]() 是奇函数.
是奇函数.
(1)求![]() 的值;
的值;
(2)证明: ![]() 为
为![]() 上的增函数;
上的增函数;
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1) ![]() ; (2)见解析;(3)
; (2)见解析;(3)![]() .
.
【解析】试题分析:(1)根据奇函数的定义,取x=1,得f(1)+f(﹣1)=0,解之得a=2,再经过检验可得当a=2时,f(x)+f(﹣x)=0对x∈R恒成立,所以f(x)是奇函数;(2)令t=2x,得![]() ,再用单调性的定义,证出当x1∈R,x2∈R且x1<x2时,y1﹣y2=
,再用单调性的定义,证出当x1∈R,x2∈R且x1<x2时,y1﹣y2=![]() ,讨论可得y1<y2,所以f(x)在R上是增函数;(3)因为f(x)是奇函数,并且在R上是增函数,所以原不等式对任意的x∈R恒成立,即mx2+1>mx﹣1对任意的x∈R恒成立,化简整理得关于m的一元二次不等式,最后经过分类讨论,可得实数m的取值范围为0≤m<8.
,讨论可得y1<y2,所以f(x)在R上是增函数;(3)因为f(x)是奇函数,并且在R上是增函数,所以原不等式对任意的x∈R恒成立,即mx2+1>mx﹣1对任意的x∈R恒成立,化简整理得关于m的一元二次不等式,最后经过分类讨论,可得实数m的取值范围为0≤m<8.
试题解析:
(1)∵函数是奇函数,
∴![]() ,
,
可得 ,解之得:
,解之得: ![]() ,
,
检验: ![]() 时,
时, ![]() ,
,
∴
∴![]() 对
对![]() 恒成立,即
恒成立,即![]() 是奇函数.
是奇函数.
∴![]()
(2)证明:令![]() ,则
,则![]()
![]()
![]()
![]()
设![]() ,
, ![]() ,且
,且![]() ,∵
,∵![]() 在
在![]() 上是增函数,∴
上是增函数,∴![]() ,
,
当![]() 时,∴
时,∴ ![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() ,可得
,可得![]() 在
在![]() 上是增函数.
上是增函数.
(3)∵![]() 是奇函数,
是奇函数,
∴不等式![]() 等价于
等价于![]()
∵![]() 在
在![]() 上是增函数,
上是增函数,
∴对任意的![]() ,原不等式恒成立,即
,原不等式恒成立,即![]() 对任意
对任意![]() 恒成立,
恒成立,
化简整理得: ![]() 对任意
对任意![]() 恒成立,
恒成立,
(1)当![]() 时,不等式即为
时,不等式即为![]() 恒成立,符合题意;
恒成立,符合题意;
(2)当![]() 时,有
时,有![]() ,即
,即![]() ,
,
综上所述:可得实数![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“世界睡眠日”定在每年的3月21日,某网站于2017年3月14日到3月20日持续一周网上调查公众日平均睡眠的时间(单位:小时),共有2 000人参加调查,现将数据整理分组后如下表所示.
序号(i)
分组睡眠时间
组中值(mi)
频数(人数)
频率(fi)
1
[4,5)
4.5
80
2
[5,6)
5.5
520
0.26
3
[6,7)
6.5
600
0.30
4
[7,8)
7.5
5
[8,9)
8.5
200
0.10
6
[9,10]
9.5
40
0.02
(1)求出表中空白处的数据,并将表格补充完整.
(2)画出频率分布直方图.
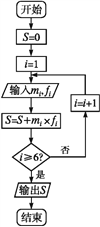
(3)为了对数据进行分析,采用了计算机辅助计算.程序框图如图所示,求输出的S值,并说明S的统计意义.
-
科目: 来源: 题型:
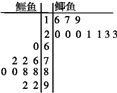
查看答案和解析>>【题目】已知某池塘养殖着鲤鱼和鲫鱼,为了估计这两种鱼的数量,养殖者从池塘中捕出这两种鱼各1 000条,给每条鱼做上不影响其存活的标记,然后放回池塘,待完全混合后,再每次从池塘中随机地捕出1 000条鱼,记录下其中有记号的鱼的数目,立即放回池塘中.这样的记录做了10次,并将记录获取的数据制作成如图所示的茎叶图.
(1)根据茎叶图计算有记号的鲤鱼和鲫鱼数目的平均数,并估计池塘中的鲤鱼和鲫鱼的数量;
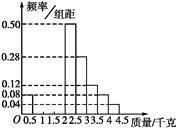
(2)为了估计池塘中鱼的总质量,现按照(1)中的比例对100条鱼进行称重,根据称重鱼的质量介于[0,4.5](单位:千克)之间,将测量结果按如下方式分成九组:第一组[0,0.5),第二组[0.5,1),…,第九组[4,4.5].如图是按上述分组方法得到的频率分布直方图的一部分.
①估计池塘中鱼的质量在3千克以上(含3千克)的条数;
②若第三组鱼的条数比第二组多7条、第四组鱼的条数比第三组多7条,请将频率分布直方图补充完整;
③在②的条件下估计池塘中鱼的质量的众数及池塘中鱼的总质量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】祖暅是南北朝时代的伟大科学家,5世纪末提出体积计算原理,即祖暅原理:“幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现有以下四个几何体:图①是从圆柱中挖出一个圆锥所得的几何体;图②、图③、图④分别是圆锥、圆台和半球,则满足祖暅原理的两个几何体为( )
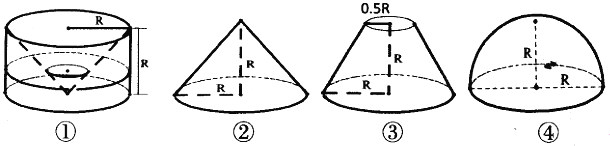
A. ①② B. ①③ C. ②④ D. ①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业为了更好地了解设备改造前后与生产合格品的关系,随机抽取了180件产品进行分析,其中设备改造前的合格品有36件,不合格品有49件,设备改造后生产的合格品有65件,不合格品有30件.根据所给数据:
⑴写出
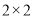 列联表;⑵判断产品是否合格与设备改造是否有关,说明理由.
列联表;⑵判断产品是否合格与设备改造是否有关,说明理由.附:
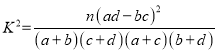 ,
, 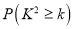
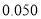
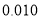
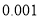
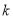
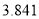
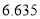
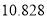
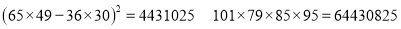
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在棱长均为4的三棱柱
 中,
中,  分别是
分别是 和
和 的中点.
的中点.
(1)求证:
 平面
平面
(2)若平面
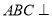 平面
平面 ,求三棱锥
,求三棱锥 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分为14分)已知定义域为R的函数
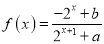 是奇函数.
是奇函数.(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
相关试题

