【题目】设椭圆C: ![]() =1(α>b>0)经过点(
=1(α>b>0)经过点( ![]() ,
, ![]() ),且原点、焦点,短轴的端点构成等腰直角三角形.
),且原点、焦点,短轴的端点构成等腰直角三角形.
(1)求椭圆E的方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线(切线斜率存在)与椭圆C恒有两个交点A,B.且 ![]() ?若存在,求出该圆的方程,若不存在说明理由.
?若存在,求出该圆的方程,若不存在说明理由.
参考答案:
【答案】
(1)解:∵原点、焦点,短轴的端点构成等腰直角三角形,∴b=c,
∵椭圆C: ![]() =1(α>b>0)经过点(
=1(α>b>0)经过点( ![]() ,
, ![]() ),∴
),∴ ![]() =1,
=1,
联立 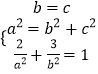 ,解得b=c=2,a2=8.
,解得b=c=2,a2=8.
∴椭圆E的方程为 ![]() =1
=1
(2)解:假设存在圆心在原点的圆,使得该圆的任意一条切线(切线斜率存在)与椭圆C恒有两个交点A,B.且 ![]() .
.
设圆的方程为:x2+y2=r2,(0<r<2).
设圆的切线为y=kx+m,则 ![]() =r,A(x1,y1),B(x2,y2).
=r,A(x1,y1),B(x2,y2).
联立 ![]() ,化为:(1+2k2)x2+4kmx+2m2﹣8=0,
,化为:(1+2k2)x2+4kmx+2m2﹣8=0,
△≥0,可得:9k2+4≥m2.
x1+x2= ![]() ,x1x2=
,x1x2= ![]() .
.
∵ ![]() ,∴
,∴ ![]() =x1x2+y1y2=0.
=x1x2+y1y2=0.
∴(1+k2)x1x2+mk(x1+x2)+m2=0,
∴ ![]() ﹣
﹣ ![]() +m2=0,
+m2=0,
化为:3m2=8+8k2,与 ![]() =r联立,
=r联立,
可得r2= ![]() =
= ![]() =
= ![]() <4,
<4,
因此假设成立,存在圆心在原点的圆,方程为x2+y2= ![]() ,使得该圆的任意一条切线(切线斜率存在)与椭圆C恒有两个交点A,B,且
,使得该圆的任意一条切线(切线斜率存在)与椭圆C恒有两个交点A,B,且 ![]()
【解析】(1)由原点、焦点,短轴的端点构成等腰直角三角形,可得b=c.由椭圆C: ![]() =1(α>b>0)经过点(
=1(α>b>0)经过点( ![]() ,
, ![]() ),可得
),可得 ![]() =1,与a2=b2+c2联立即可得出.(2)假设存在圆心在原点的圆,使得该圆的任意一条切线(切线斜率存在)与椭圆C恒有两个交点A,B.且
=1,与a2=b2+c2联立即可得出.(2)假设存在圆心在原点的圆,使得该圆的任意一条切线(切线斜率存在)与椭圆C恒有两个交点A,B.且 ![]() .设圆的方程为:x2+y2=r2 , (0<r<2).设圆的切线为y=kx+m,可得
.设圆的方程为:x2+y2=r2 , (0<r<2).设圆的切线为y=kx+m,可得 ![]() =r,A(x1 , y1),B(x2 , y2).与椭圆方程联立化为:(1+2k2)x2+4kmx+2m2﹣8=0,利用根与系数的关系及其
=r,A(x1 , y1),B(x2 , y2).与椭圆方程联立化为:(1+2k2)x2+4kmx+2m2﹣8=0,利用根与系数的关系及其 ![]() ,可得
,可得 ![]() =x1x2+y1y2=0.化简整理即可得出.
=x1x2+y1y2=0.化简整理即可得出.
-
科目: 来源: 题型:
查看答案和解析>>【题目】袋子中装有除颜色外其他均相同的编号为a,b的两个黑球和编号为c,d,e的三个红球,从中任意摸出两个球.
(1)求恰好摸出1个黑球和1个红球的概率:
(2)求至少摸出1个黑球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校研究性学习小组从汽车市场上随机抽取
 辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于
辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于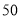 公里和
公里和 公里之间,将统计结果分成
公里之间,将统计结果分成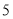 组:
组: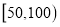 ,
, ,
, ,
, ,
, ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.
(1)求直方图中
 的值;
的值;(2)求续驶里程在
 的车辆数;
的车辆数;(3)若从续驶里程在
 的车辆中随机抽取
的车辆中随机抽取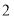 辆车,求其中恰有一辆车的续驶里程在
辆车,求其中恰有一辆车的续驶里程在 内的概率.
内的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直三棱柱ABC﹣A1B1C1中,AA1=AB=AC=2,D,E,F分别是B1A1 , CC1 , BC的中点,AE⊥A1B1 , D为棱A1B1上的点.

(1)证明:DF⊥AE;
(2)求平面DEF与平面ABC所成锐二面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=xlnx﹣ax2+(2a﹣1)x.
(1)若a= ,求函数f(x)的单调区间;
,求函数f(x)的单调区间;
(2)若x∈[1,+∞)时恒有f(x)≤a﹣1,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
 中,侧面
中,侧面 是边长为2的正方形,点
是边长为2的正方形,点 是棱
是棱 的中点.
的中点.
(1)证明:
 平面
平面 .
.(2)若三棱锥
 的体积为4,求点
的体积为4,求点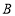 到平面
到平面 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】现从某医院中随机抽取了七位医护人员的关爱患者考核分数(患者考核:10分制),用相关的特征量
 表示;医护专业知识考核分数(试卷考试:100分制),用相关的特征量
表示;医护专业知识考核分数(试卷考试:100分制),用相关的特征量 表示,数据如下表:
表示,数据如下表:(Ⅰ)求
 关于
关于 的线性回归方程(计算结果精确到0.01);
的线性回归方程(计算结果精确到0.01);(Ⅱ)利用(I)中的线性回归方程,分析医护专业考核分数的变化对关爱患者考核分数的影响,并估计某医护人员的医护专业知识考核分数为95分时,他的关爱患者考核分数(精确到0.1);

(Ⅲ)现要从医护专业知识考核分数95分以下的医护人员中选派2人参加组建的“九寨沟灾后医护小分队”培训,求这两人中至少有一人考核分数在90分以下的概率.
附:回归方程
 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为
相关试题

