【题目】已知函数f(x)=xlnx﹣ax2+(2a﹣1)x.
(1)若a= ![]() ,求函数f(x)的单调区间;
,求函数f(x)的单调区间;
(2)若x∈[1,+∞)时恒有f(x)≤a﹣1,求a的取值范围.
参考答案:
【答案】
(1)解:a= ![]() 时,f(x)=xlnx﹣
时,f(x)=xlnx﹣ ![]() x2,x>0.
x2,x>0.
f(x)的导数为f′(x)=1+lnx﹣x,
令g(x)=1+lnx﹣x,g′(x)= ![]() ﹣1,
﹣1,
当x>1时,g′(x)<0,g(x)递减;当0<x<1时,g′(x)>0,g(x)递增.
即有g(x)在x=1处取得极大值,且为最大值0.
则g(x)≤0,即1+lnx﹣x≤0,
即f′(x)≤0,则f(x)在(0,+∞)递减.
综上可得,f(x)的减区间为(0,+∞),无增区间
(2)解:当x≥1时,f(x)≤a﹣1,
即为xlnx﹣ax2+(2a﹣1)x≤a﹣1,
当x=1时,上式显然成立.
当x>1时,可得a≥ ![]() .
.
由 ![]() ﹣1=
﹣1= ![]() ,
,
设g(x)=xlnx﹣(x﹣1)﹣(x﹣1)2(x>1),
g′(x)=1+lnx﹣1﹣2(x﹣1)=lnx﹣2(x﹣1),
由g″(x)= ![]() ﹣2<0在x>1恒成立,
﹣2<0在x>1恒成立,
可得g′(x)在(1,+∞)递减,可得g′(x)<g′(1)=0,
即g(x)在(1,+∞)递减,可得g(x)<g(1)=0,
则 ![]() <1成立,
<1成立,
即有a≥1.
即a的范围是[1,+∞).
【解析】(1)求得f(x)的解析式,求出导数,令g(x)=1+lnx﹣x,求出导数,单调区间和最大值,即可得到f(x)的单调区间;(2)当x≥1时,f(x)≤a﹣1,即为xlnx﹣ax2+(2a﹣1)x≤a﹣1,讨论x=1和x>1,由参数分离和构造函数g(x)=xlnx﹣(x﹣1)﹣(x﹣1)2(x>1),求出导数和单调性,即可判断g(x)的单调性,可得a的范围.
【考点精析】根据题目的已知条件,利用利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识可以得到问题的答案,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校研究性学习小组从汽车市场上随机抽取
 辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于
辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于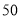 公里和
公里和 公里之间,将统计结果分成
公里之间,将统计结果分成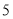 组:
组: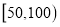 ,
, ,
, ,
, ,
, ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.
(1)求直方图中
 的值;
的值;(2)求续驶里程在
 的车辆数;
的车辆数;(3)若从续驶里程在
 的车辆中随机抽取
的车辆中随机抽取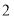 辆车,求其中恰有一辆车的续驶里程在
辆车,求其中恰有一辆车的续驶里程在 内的概率.
内的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直三棱柱ABC﹣A1B1C1中,AA1=AB=AC=2,D,E,F分别是B1A1 , CC1 , BC的中点,AE⊥A1B1 , D为棱A1B1上的点.

(1)证明:DF⊥AE;
(2)求平面DEF与平面ABC所成锐二面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆C:
 =1(α>b>0)经过点(
=1(α>b>0)经过点(  ,
,  ),且原点、焦点,短轴的端点构成等腰直角三角形.
),且原点、焦点,短轴的端点构成等腰直角三角形.
(1)求椭圆E的方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线(切线斜率存在)与椭圆C恒有两个交点A,B.且 ?若存在,求出该圆的方程,若不存在说明理由.
?若存在,求出该圆的方程,若不存在说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
 中,侧面
中,侧面 是边长为2的正方形,点
是边长为2的正方形,点 是棱
是棱 的中点.
的中点.
(1)证明:
 平面
平面 .
.(2)若三棱锥
 的体积为4,求点
的体积为4,求点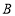 到平面
到平面 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】现从某医院中随机抽取了七位医护人员的关爱患者考核分数(患者考核:10分制),用相关的特征量
 表示;医护专业知识考核分数(试卷考试:100分制),用相关的特征量
表示;医护专业知识考核分数(试卷考试:100分制),用相关的特征量 表示,数据如下表:
表示,数据如下表:(Ⅰ)求
 关于
关于 的线性回归方程(计算结果精确到0.01);
的线性回归方程(计算结果精确到0.01);(Ⅱ)利用(I)中的线性回归方程,分析医护专业考核分数的变化对关爱患者考核分数的影响,并估计某医护人员的医护专业知识考核分数为95分时,他的关爱患者考核分数(精确到0.1);

(Ⅲ)现要从医护专业知识考核分数95分以下的医护人员中选派2人参加组建的“九寨沟灾后医护小分队”培训,求这两人中至少有一人考核分数在90分以下的概率.
附:回归方程
 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为
-
科目: 来源: 题型:
查看答案和解析>>【题目】某实验单次成功的概率为0.8,记事件A为“在实验条件相同的情况下,重复3次实验,各次实验互不影响,则3次实验中至少成功2次”,现采用随机模拟的方法估计事件4的概率:先由计算机给出0~9十个整数值的随机数,指定0,1表示单次实验失败,2,3,4,5,6,7,8,9表示单次实验成功,以3个随机数为组,代表3次实验的结果经随机模拟产生了20组随机数,如下表:
752
029
714
985
034
437
863
694
141
469
037
623
804
601
366
959
742
761
428
261
根据以上方法及数据,估计事件A的概率为( )
A.0.384B.0.65C.0.9D.0.904
相关试题

