【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求
时,求![]() 的极值;
的极值;
(Ⅱ)若曲线![]() 在点
在点![]() 处切线的斜率为3,且
处切线的斜率为3,且![]() 对任意
对任意![]() 都成立,求整数
都成立,求整数![]() 的最大值.
的最大值.
参考答案:
【答案】(Ⅰ) 极小值![]() ;(Ⅱ)4.
;(Ⅱ)4.
【解析】
试题分析:(Ⅰ)求出导数![]() ,令
,令![]() ,求出根,讨论这些根的两边
,求出根,讨论这些根的两边![]() 的符号,可得极值;(Ⅱ)由导数的几何意义可求得参数
的符号,可得极值;(Ⅱ)由导数的几何意义可求得参数![]() ,这样且
,这样且![]() 对任意
对任意![]() 恒成立,可化为
恒成立,可化为![]() 在
在![]() 上恒成立,这样我们只要求函数
上恒成立,这样我们只要求函数![]() 的最小值即可,当然题目要求整数
的最小值即可,当然题目要求整数![]() 的最大值,故可求最小值的范围,为了讨论
的最大值,故可求最小值的范围,为了讨论![]() 的正负,可能还要对
的正负,可能还要对![]() (或其中部分式子)再求导,通过研究
(或其中部分式子)再求导,通过研究![]() (或其中部分式子)的导数,一步步研究得出结论.
(或其中部分式子)的导数,一步步研究得出结论.
试题解析:(Ⅰ) ![]() 时,
时,![]()
∴![]() ∴
∴![]()
当x变化时,![]() 与
与![]() 变化如下表:
变化如下表:
X |
|
|
|
| - | 0 | + |
| 递减 | 极小值 | 递增 |
∴当![]() 时,
时,![]() 有极小值
有极小值![]() .
.
(Ⅱ)易求得![]() 故问题化为
故问题化为![]() 在
在![]() 上恒成立
上恒成立
令![]() ,则
,则![]()
又令![]() ,
,
则![]() 在
在![]() 上恒成立,
上恒成立,
∴![]() 在
在![]() 递增,
递增,
又∵![]()
∴![]() 在
在![]() 上有唯一零点,设为
上有唯一零点,设为![]() ,则
,则![]()
且![]() ①
①
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减,
∴![]()
![]() ,将①代入有
,将①代入有
![]()
所以![]() 所以整数b的最大值为4.
所以整数b的最大值为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
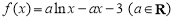 .
.(Ⅰ)当
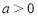 时,求函数
时,求函数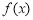 的单调区间;
的单调区间;(Ⅱ)若函数
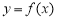 的图象在点
的图象在点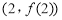 处的切线的倾斜角为
处的切线的倾斜角为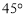 ,且函数
,且函数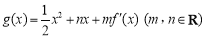 当且仅当在
当且仅当在 处取得极值,其中
处取得极值,其中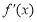 为
为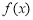 的导函数,求
的导函数,求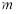 的取值范围;
的取值范围; -
科目: 来源: 题型:
查看答案和解析>>【题目】某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加了其中一组,在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的
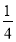 ,且该组中,青年人占50%,中年人占40%,老年人占10%.为了了解各组不同年龄层次的职工对本次活动的满意程度,现用分层抽样方法从参加活动的全体职工中抽取一个容量为200的样本,试确定:
,且该组中,青年人占50%,中年人占40%,老年人占10%.为了了解各组不同年龄层次的职工对本次活动的满意程度,现用分层抽样方法从参加活动的全体职工中抽取一个容量为200的样本,试确定:(1)游泳组中,青年人、中年人、老年人分别所占的比例;
(2)游泳组中,青年人、中年人、老年人分别应抽取的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区有小学21所,中学14所,大学7所,现采用分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查.
(1)求应从小学、中学、大学中分别抽取的学校数目;
(2)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
①列出所有可能的抽取结果;
②求抽取的2所学校均为小学的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
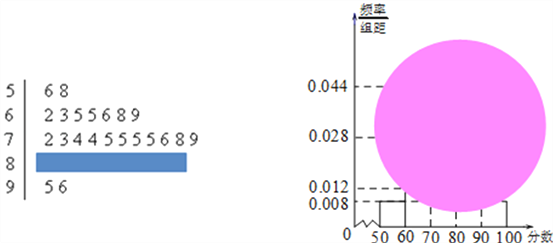
(Ⅰ)求分数在[50,60)的频率及全班人数;
(Ⅱ)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间矩形的高;
(Ⅲ)若要从分数在[80,100)之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在[90,100)之间的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是锐角三角形,cos22A+sin2A=1.
(Ⅰ)求角A;
(Ⅱ)若BC=1,B=x,求△ABC的周长f(x)的单调区间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某地参加2015 年夏令营的
 名学生的身体健康情况,将学生编号为
名学生的身体健康情况,将学生编号为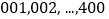 ,采用系统抽样的方法抽取一个容量为
,采用系统抽样的方法抽取一个容量为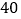 的样本,且抽到的最小号码为
的样本,且抽到的最小号码为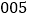 ,已知这
,已知这 名学生分住在三个营区,从
名学生分住在三个营区,从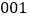 到
到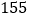 在第一营区,从
在第一营区,从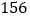 到
到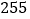 在第二营区,从
在第二营区,从 到
到 在第三营区,则第一、第二、第三营区被抽中的人数分别为( )
在第三营区,则第一、第二、第三营区被抽中的人数分别为( )A.
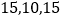 B.
B.  C.
C.  D.
D. 
相关试题

