【题目】如图,已知等边![]() 的边长为4,,
的边长为4,,![]() 分别为
分别为![]() 边的中点,
边的中点,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 边上一点,且
边上一点,且![]() ,将
,将![]() 沿
沿![]() 折到
折到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)设![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
参考答案:
【答案】详见解析.
【解析】
试题分析:(1)首先根据已知条件可证出![]() ,再由面面垂直的性质定理并结合平面
,再由面面垂直的性质定理并结合平面![]() 平面
平面![]() 可得出
可得出![]() 平面
平面![]() ,然后再由
,然后再由![]() 和
和![]() 可证得
可证得![]() ,再在正
,再在正![]() 中易证得
中易证得![]() 平面
平面![]() ,最后由面面垂直的判定定理即可得出所证的结论;
,最后由面面垂直的判定定理即可得出所证的结论;
(2)首先由(1)可知,![]() 平面
平面![]() ,即
,即![]() 为
为![]() 三棱锥底面上的高,然后结合已知可得出
三棱锥底面上的高,然后结合已知可得出![]() ,
,![]() ,
,![]() ,进而可得
,进而可得![]() ,最后由三棱锥的体积计算公式即可得出所求的结果.
,最后由三棱锥的体积计算公式即可得出所求的结果.
试题解析:(1)因为![]() ,
,![]() 为等边
为等边![]() 的
的![]() ,
,![]() 边的中点,
边的中点,
所以![]() 是等边三角形,且
是等边三角形,且![]() .因为
.因为![]() 是
是![]() 的中点,所以
的中点,所以![]() .
.
又由于平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以
,所以![]() .因为
.因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
在正![]() 中知
中知![]() ,所以
,所以![]() .而
.而![]() ,所以
,所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)由(1)知,![]() 平面
平面![]() ,所以
,所以![]() 为
为![]() 三棱锥底面上的高.
三棱锥底面上的高.
根据正三角形的边长为4,知![]() 是边长为2的等边三角形,所以
是边长为2的等边三角形,所以![]() .
.
易知![]() ,
,![]() .
.
又由(1)知![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数据
 ,
, ,
, ,…,
,…, 是杭州市100个普通职工的2016年10月份的收入(均不超过2万元),设这100个数据的中位数为
是杭州市100个普通职工的2016年10月份的收入(均不超过2万元),设这100个数据的中位数为 ,平均数为
,平均数为 ,方差为
,方差为 ,如果再加上马云2016年10月份的收入
,如果再加上马云2016年10月份的收入 (约100亿元),则相对于
(约100亿元),则相对于 、
、 、
、 ,这101个月收入数据( )
,这101个月收入数据( )A. 平均数可能不变,中位数可能不变,方差可能不变
B. 平均数大大增大,中位数可能不变,方差也不变
C. 平均数大大增大,中位数一定变大,方差可能不变
D. 平均数大大增大,中位数可能不变,方差变大
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司过去五个月的广告费支出
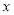 与销售额
与销售额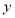 (单位:万元)之间有下列对应数据:
(单位:万元)之间有下列对应数据: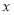
2
4
5
6
8
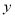

40
60
50
70
工作人员不慎将表格中
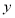 的第一个数据丢失.已知
的第一个数据丢失.已知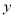 对
对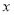 呈线性相关关系,且回归方程为
呈线性相关关系,且回归方程为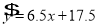 ,则下列说法:①销售额
,则下列说法:①销售额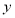 与广告费支出
与广告费支出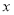 正相关;②丢失的数据(表中
正相关;②丢失的数据(表中 处)为30;③该公司广告费支出每增加1万元,销售额一定增加
处)为30;③该公司广告费支出每增加1万元,销售额一定增加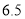 万元;④若该公司下月广告投入8万元,则销售
万元;④若该公司下月广告投入8万元,则销售额为70万元.其中,正确说法有( )
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.圆锥的底面是圆面,侧面是曲面
B.用一张扇形的纸片可以卷成一个圆锥
C.一个物体上、下两个面是相等的圆面,那么它一定是一个圆柱
D.圆台的任意两条母线的延长线可能相交也可能不相交
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 是等比数列,
是等比数列,  为数列
为数列 的前
的前 项和,且
项和,且
(1)求数列
 的通项公式.
的通项公式.(2)设
 且
且 为递增数列.若
为递增数列.若 求证:
求证: 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 中,首项
中,首项 ,
,  .
.(1)求证:数列
 是等比数列;
是等比数列;(2)求数列
 的通项公式
的通项公式 以及前
以及前 项和
项和
-
科目: 来源: 题型:
查看答案和解析>>【题目】将函数
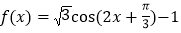 的图象向左平移
的图象向左平移 个单位长度,再向上平移1个单位长度,得到函数
个单位长度,再向上平移1个单位长度,得到函数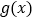 的图象,则函数
的图象,则函数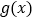 具有性质__________.(填入所有正确性质的序号)
具有性质__________.(填入所有正确性质的序号)①最大值为
 ,图象关于直线
,图象关于直线 对称;
对称;②图象关于
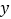 轴对称;
轴对称;③最小正周期为
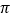 ;
;④图象关于点
 对称;
对称;⑤在
 上单调递减
上单调递减
相关试题

