【题目】已知数列![]() 中,首项
中,首项![]() ,
, ![]() .
.
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)求数列![]() 的通项公式
的通项公式![]() 以及前
以及前![]() 项和
项和![]()
参考答案:
【答案】(1)证明过程见解析;(2)![]()
【解析】试题分析:(1)由![]() ,变形为:
,变形为: ![]() ,且
,且![]() ,利用等比数列的通项公式及其定义即可得出;(2)由数列
,利用等比数列的通项公式及其定义即可得出;(2)由数列![]() 的通项公式 ,利用分组求和法及等比数列与等差数列的前
的通项公式 ,利用分组求和法及等比数列与等差数列的前![]() 和公式即可得出.
和公式即可得出.
试题解析:(1)证明: ![]()
![]()
![]()
又![]()
![]() 是以6为首项,以2为公比的等比数列
是以6为首项,以2为公比的等比数列
(2)由(1)知: ![]()
![]()
![]()
【方法点晴】本题主要考查等比数列的定义、等比数列的通项及利用“分组求和法”求数列前![]() 项和,属于中档题. 利用“分组求和法”求数列前
项和,属于中档题. 利用“分组求和法”求数列前![]() 项和常见类型有两种:一是通项为两个公比不相等的等比数列的和或差,可以分别用等比数列求和后再相加减;二是通项为一个等差数列和一个等比数列的和或差,可以分别用等差数列求和、等比数列求和后再相加减.
项和常见类型有两种:一是通项为两个公比不相等的等比数列的和或差,可以分别用等比数列求和后再相加减;二是通项为一个等差数列和一个等比数列的和或差,可以分别用等差数列求和、等比数列求和后再相加减.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.圆锥的底面是圆面,侧面是曲面
B.用一张扇形的纸片可以卷成一个圆锥
C.一个物体上、下两个面是相等的圆面,那么它一定是一个圆柱
D.圆台的任意两条母线的延长线可能相交也可能不相交
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等边
 的边长为4,,
的边长为4,, 分别为
分别为 边的中点,
边的中点, 为
为 的中点,
的中点, 为
为 边上一点,且
边上一点,且 ,将
,将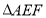 沿
沿 折到
折到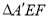 的位置,使平面
的位置,使平面 平面
平面 .
.
(1)求证:平面
 平面
平面 ;
;(2)设
 ,求三棱锥
,求三棱锥 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 是等比数列,
是等比数列,  为数列
为数列 的前
的前 项和,且
项和,且
(1)求数列
 的通项公式.
的通项公式.(2)设
 且
且 为递增数列.若
为递增数列.若 求证:
求证: 
-
科目: 来源: 题型:
查看答案和解析>>【题目】将函数
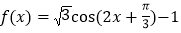 的图象向左平移
的图象向左平移 个单位长度,再向上平移1个单位长度,得到函数
个单位长度,再向上平移1个单位长度,得到函数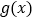 的图象,则函数
的图象,则函数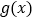 具有性质__________.(填入所有正确性质的序号)
具有性质__________.(填入所有正确性质的序号)①最大值为
 ,图象关于直线
,图象关于直线 对称;
对称;②图象关于
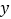 轴对称;
轴对称;③最小正周期为
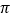 ;
;④图象关于点
 对称;
对称;⑤在
 上单调递减
上单调递减 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在边长为1的正方形
 内任取一点
内任取一点 ,求事件“
,求事件“ ”的概率;(2)某班在一次数学活动中,老师让全班56名同学每人随机写下一对都小于1的正实数
”的概率;(2)某班在一次数学活动中,老师让全班56名同学每人随机写下一对都小于1的正实数 、
、 ,统计出两数能与1构成锐角三角形的三边长的数对
,统计出两数能与1构成锐角三角形的三边长的数对 共有12对,请据此估计
共有12对,请据此估计 的近似值(精确到
的近似值(精确到 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】某制造厂商10月份生产了一批乒乓球,从中随机抽取
 个进行检查,测得每个球的直径(单位:
个进行检查,测得每个球的直径(单位: ),将数据进行分组,得到如下频率分布表:
),将数据进行分组,得到如下频率分布表:
(1)求
 、
、 、
、 及
及 、
、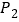 的值,并画出频率分布直方图(结果保留两位小数);
的值,并画出频率分布直方图(结果保留两位小数);(2)已知标准乒乓球的直径为
 ,直径误差不超过
,直径误差不超过 的为五星乒乓球,若这批乒乓球共有
的为五星乒乓球,若这批乒乓球共有 个,试估计其中五星乒乓球的数目;
个,试估计其中五星乒乓球的数目;(3)统计方法中,同一组数据常用该组区间的中点值(例如区间
 的中点值是
的中点值是 )作为代表,估计这批乒乓球直径的平均值和中位数.
)作为代表,估计这批乒乓球直径的平均值和中位数.
相关试题

