【题目】已知数列![]() 是等比数列,
是等比数列, ![]() 为数列
为数列![]() 的前
的前![]() 项和,且
项和,且![]()
(1)求数列![]() 的通项公式.
的通项公式.
(2)设![]() 且
且![]() 为递增数列.若
为递增数列.若![]() 求证:
求证: ![]()
参考答案:
【答案】(1)当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ;(2)证明过程见解析;
;(2)证明过程见解析;
【解析】试题分析:(1)设数列![]() 的公式为
的公式为![]() ,从而可得
,从而可得![]() ,求出
,求出![]() 的值,从而可得结果;(2)讨论可知
的值,从而可得结果;(2)讨论可知![]() ,考虑
,考虑![]() 为递增数列,从而可得
为递增数列,从而可得![]() ,利用裂项相消法求和,再用放缩法证明即可.
,利用裂项相消法求和,再用放缩法证明即可.
试题解析:(1)设等比数列![]() 的公比为
的公比为![]() .由已知:
.由已知: ![]()
![]() ,解得
,解得![]() 或
或![]()
当![]() 时,
时, ![]()
当![]() 时,
时, ![]()
(2)![]() 为递增数列,
为递增数列, ![]() 不合题意
不合题意
当![]() 时,
时, ![]() 符合题意.
符合题意.
![]()
![]()
【方法点晴】裂项相消法是最难把握的求和方法之一,其原因是有时很难找到裂项的方向,突破这一难点的方法是根据式子的结构特点,掌握一些常见的裂项技巧:①![]() ;②
;②![]()
![]() ;③
;③![]() ;
;
④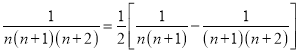 ;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司过去五个月的广告费支出
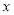 与销售额
与销售额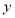 (单位:万元)之间有下列对应数据:
(单位:万元)之间有下列对应数据:
2
4
5
6
8
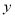

40
60
50
70
工作人员不慎将表格中
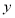 的第一个数据丢失.已知
的第一个数据丢失.已知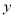 对
对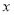 呈线性相关关系,且回归方程为
呈线性相关关系,且回归方程为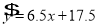 ,则下列说法:①销售额
,则下列说法:①销售额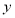 与广告费支出
与广告费支出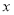 正相关;②丢失的数据(表中
正相关;②丢失的数据(表中 处)为30;③该公司广告费支出每增加1万元,销售额一定增加
处)为30;③该公司广告费支出每增加1万元,销售额一定增加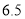 万元;④若该公司下月广告投入8万元,则销售
万元;④若该公司下月广告投入8万元,则销售额为70万元.其中,正确说法有( )
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.圆锥的底面是圆面,侧面是曲面
B.用一张扇形的纸片可以卷成一个圆锥
C.一个物体上、下两个面是相等的圆面,那么它一定是一个圆柱
D.圆台的任意两条母线的延长线可能相交也可能不相交
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等边
 的边长为4,,
的边长为4,, 分别为
分别为 边的中点,
边的中点, 为
为 的中点,
的中点, 为
为 边上一点,且
边上一点,且 ,将
,将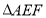 沿
沿 折到
折到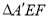 的位置,使平面
的位置,使平面 平面
平面 .
.
(1)求证:平面
 平面
平面 ;
;(2)设
 ,求三棱锥
,求三棱锥 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 中,首项
中,首项 ,
,  .
.(1)求证:数列
 是等比数列;
是等比数列;(2)求数列
 的通项公式
的通项公式 以及前
以及前 项和
项和
-
科目: 来源: 题型:
查看答案和解析>>【题目】将函数
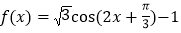 的图象向左平移
的图象向左平移 个单位长度,再向上平移1个单位长度,得到函数
个单位长度,再向上平移1个单位长度,得到函数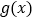 的图象,则函数
的图象,则函数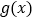 具有性质__________.(填入所有正确性质的序号)
具有性质__________.(填入所有正确性质的序号)①最大值为
 ,图象关于直线
,图象关于直线 对称;
对称;②图象关于
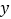 轴对称;
轴对称;③最小正周期为
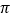 ;
;④图象关于点
 对称;
对称;⑤在
 上单调递减
上单调递减 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在边长为1的正方形
 内任取一点
内任取一点 ,求事件“
,求事件“ ”的概率;(2)某班在一次数学活动中,老师让全班56名同学每人随机写下一对都小于1的正实数
”的概率;(2)某班在一次数学活动中,老师让全班56名同学每人随机写下一对都小于1的正实数 、
、 ,统计出两数能与1构成锐角三角形的三边长的数对
,统计出两数能与1构成锐角三角形的三边长的数对 共有12对,请据此估计
共有12对,请据此估计 的近似值(精确到
的近似值(精确到 ).
).
相关试题

