【题目】已知实数a≠0,函数f(x)= ![]() ,若f(1﹣a)=f(1+a),则a的值为( )
,若f(1﹣a)=f(1+a),则a的值为( )
A.﹣ ![]()
B.﹣ ![]()
C.﹣ ![]() 或﹣
或﹣ ![]()
D.﹣1
参考答案:
【答案】B
【解析】解:∵实数a≠0,函数f(x)= ![]() ,f(1﹣a)=f(1+a),
,f(1﹣a)=f(1+a),
∴若a>0,则1﹣a<1,1+a>1,又f(1﹣a)=f(1+a),
∴2(1﹣a)+a=﹣(1+a)﹣2a,解得a=﹣ ![]() ,不成立;
,不成立;
若a<0,则1﹣a>1,1+a<1,又f(1﹣a)=f(1+a),
∴2(1+a)+a=﹣(1﹣a)﹣2a,解得a=﹣ ![]() .
.
∴a=﹣ ![]() .
.
故选:B.
【考点精析】认真审题,首先需要了解函数的值(函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农科所发现,一种作物的年收获量
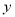 (单位:
(单位: 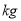 )与它“相近”作物的株数
)与它“相近”作物的株数 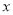 具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过
具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过 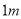 ),并分别记录了相近作物的株数为
),并分别记录了相近作物的株数为 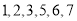 时,该作物的年收获量的相关数据如下:
时,该作物的年收获量的相关数据如下: 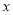
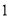
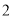
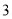
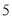
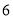
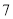
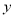
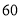
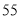
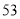
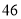
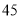
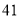
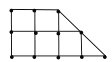
(1)求该作物的年收获量
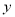 关于它“相近”作物的株数
关于它“相近”作物的株数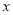 的线性回归方程;
的线性回归方程;(2)农科所在如图所示的直角梯形地块的每个格点(指纵、横直线的交叉点)处都种了一株该作物,图中
每个小正方形的边长均为
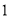 ,若从直角梯形地块的边界和内部各随机选取一株该作物,求这两株作物 “相
,若从直角梯形地块的边界和内部各随机选取一株该作物,求这两株作物 “相近”且年产量仅相差
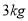 的概率.
的概率.附:对于一组数据
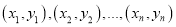 ,其回归直线
,其回归直线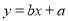 的斜率和截距的最小二乘估
的斜率和截距的最小二乘估计分别为,
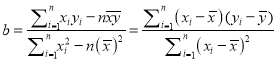 ,
, 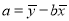
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
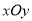 中,二次函数
中,二次函数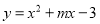 的图象与
的图象与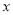 轴交于
轴交于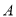 ,
, 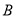 两点,点
两点,点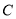 的坐标为
的坐标为 .当
.当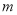 变化时,解答下列问题:
变化时,解答下列问题:(1)以
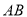 为直径的圆能否经过点
为直径的圆能否经过点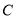 ?说明理由;
?说明理由;(2)过
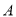 ,
, 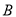 ,
, 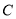 三点的圆在
三点的圆在 轴上截得的弦长是否为定值?若是,则求出该定值;若不是,请说明理由.
轴上截得的弦长是否为定值?若是,则求出该定值;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接2017年“双
 ”,“双
”,“双 ”购物狂欢节的来临,某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共
”购物狂欢节的来临,某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共 个,生产一个汤碗需
个,生产一个汤碗需 分钟,生产一个花瓶需
分钟,生产一个花瓶需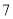 分钟,生产一个茶杯需
分钟,生产一个茶杯需 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过 小时.若生产一个汤碗可获利润
小时.若生产一个汤碗可获利润 元,生产一个花瓶可获利润
元,生产一个花瓶可获利润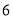 元,生产一个茶杯可获利润
元,生产一个茶杯可获利润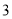 元.
元.(1)使用每天生产的汤碗个数
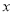 与花瓶个数
与花瓶个数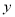 表示每天的利润
表示每天的利润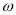 (元);
(元);(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系中,以原点为极点,
 轴正半轴为极轴建立坐标系,直线
轴正半轴为极轴建立坐标系,直线 的极坐标方程为
的极坐标方程为 ,曲线
,曲线 的参数方程为
的参数方程为 ,(
,(  为参数).
为参数).(Ⅰ)求直线
 的直角坐标方程和曲线
的直角坐标方程和曲线 的普通方程;
的普通方程;(Ⅱ)曲线
 交
交 轴于
轴于 两点,且点
两点,且点 ,
,  为直线
为直线 上的动点,求
上的动点,求 周长的最小值.
周长的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
 的底面为平行四边形,且
的底面为平行四边形,且 ,
, ,
, 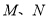 分别为
分别为 中点,过
中点,过 作平面
作平面 分别与线段
分别与线段 相交于点
相交于点 .
.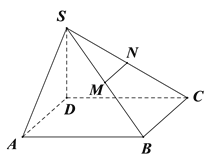
(Ⅰ)在图中作出平面
 使面
使面 ‖
‖ (不要求证明);
(不要求证明);(II)若
 ,在(Ⅰ)的条件下求多面体
,在(Ⅰ)的条件下求多面体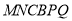 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 的顶点
的顶点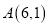 ,
, 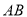 边上的中线
边上的中线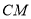 所在直线方程为
所在直线方程为 ,
, 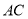 边上的高
边上的高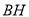 所在直线方程为
所在直线方程为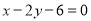 .
. (1)求点
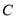 的坐标;
的坐标;(2)求直线
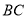 的方程.
的方程.
相关试题

