【题目】已知![]() ,
,![]() 是实数,函数
是实数,函数![]() ,
,![]() ,若
,若![]() 在区间
在区间![]() 上恒成立,则称
上恒成立,则称![]() 和
和![]() 在区间
在区间![]() 上为“
上为“![]() 函数”.
函数”.
(1)设![]() ,若
,若![]() 和
和![]() 在区间
在区间![]() 上为“
上为“![]() 函数”,求实数
函数”,求实数![]() 的取值范围;
的取值范围;
(2)设![]() ,
,![]() 且
且![]() ,若
,若![]() 和
和![]() 在以
在以![]() ,
,![]() 为端点的开区间上为“
为端点的开区间上为“![]() 函数”,求
函数”,求![]() 的最大值.
的最大值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)按照“![]() 函数”的定义,将函数表达式代入
函数”的定义,将函数表达式代入![]() ,化简得
,化简得![]() ,所以有
,所以有![]() ,解得
,解得![]() ;(2)分别按
;(2)分别按![]() ,
,![]() 两类,结合“
两类,结合“![]() 函数”的定义,类似(1)的方法,讨论得
函数”的定义,类似(1)的方法,讨论得![]() 的最大值为
的最大值为![]() .
.
试题解析:
(1)因为![]() 和
和![]() 在区间
在区间![]() 上为“
上为“![]() 函数”,
函数”,
所以![]() ,在
,在![]() 上恒成立,
上恒成立,
即![]() ,
,![]()
![]() ,
,![]()
![]() ,即
,即![]() ,
,![]() ,
,![]() .……………(4分)
.……………(4分)
(2)①当![]() 时,因为
时,因为![]() 和
和![]() 在以
在以![]() ,
,![]() 为端点的开区间上为“
为端点的开区间上为“![]() 函数”,
函数”,
所以,![]() 在
在![]() 上恒成立,
上恒成立,
即![]() ,
,![]() 恒成立,
恒成立,
![]() ,
,![]() 对任意
对任意![]() ,
,![]() ,
,
故对任意![]() ,
,![]() ,
,
![]() ,
,
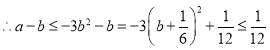 .………………(8分)
.………………(8分)
②当![]() 时,因为
时,因为![]() 和
和![]() 在以
在以![]() ,
,![]() 为端点的开区间上为“
为端点的开区间上为“![]() 函数”,所以
函数”,所以![]() 在
在![]() 上恒成立,
上恒成立,
即![]() ,
,![]() 恒成立,
恒成立,
![]() ,
,![]() 对任意
对任意![]() ,
,![]() ,
,
故对任意![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
综上可知,![]() .……………………………(12分)
.……………………………(12分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】从某校高三上学期期末数学考试成绩中,随机抽取了
 名学生的成绩得到频率分布直方图如下:
名学生的成绩得到频率分布直方图如下:
(1)根据频率分布直方图,估计该校高三学生本次数学考试的平均分;
(2)若用分层抽样的方法从分数在
 和
和 的学生中共抽取
的学生中共抽取 人,该
人,该 人中成绩在
人中成绩在 的有几人?
的有几人?(3)在(2)中抽取的
 人中,随机抽取
人中,随机抽取 人,求分数在
人,求分数在 和
和 各
各 人的概率.
人的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明:“自然数a,b,c中恰有一个偶数”时正确的反设为 ( )
A. a,b,c都是偶数
B. a,b,c都是奇数
C. a,b,c中至少有两个偶数
D. a,b,c中都是奇数或至少有两个偶数
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班的60名同学已编号1,2,3,…,60,为了解该班同学的作业情况,老师收取了号码能被5整除的12名同学的作业本,这里运用的抽样方法是( )
A. 简单随机抽样 B. 系统抽样
C. 分层抽样 D. 抽签法
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 .
.(1)当a=2时,判断函数
 在定义域内的单调性;
在定义域内的单调性;(2)当
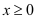 时,
时,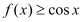 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】对某电子元件进行寿命追踪调查,所得样本数据的频率分布直方图如下.

(1)求
 ,并根据图中的数据,用分层抽样的方法抽取
,并根据图中的数据,用分层抽样的方法抽取 个元件,元件寿命落在
个元件,元件寿命落在 之间的应抽取几个?
之间的应抽取几个?(2)从(1)中抽出的寿命落在
 之间的元件中任取
之间的元件中任取 个元件,求事件“恰好有一个元件寿命落在
个元件,求事件“恰好有一个元件寿命落在 之间,一个元件寿命落在
之间,一个元件寿命落在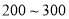 之间”的概率.
之间”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的左、右焦点分别为
的左、右焦点分别为 ,P为椭圆C上任意一点,且
,P为椭圆C上任意一点,且 最小值为0.
最小值为0.(1)求曲线C的方程;
(2)若动直线
 均与椭圆C相切,且
均与椭圆C相切,且 ,试探究在x轴上是否存在定点B,使得点B到
,试探究在x轴上是否存在定点B,使得点B到 的距离之积恒为1?若存在,请求出点B的坐标;若不存在,请说明理由.
的距离之积恒为1?若存在,请求出点B的坐标;若不存在,请说明理由.
相关试题

