【题目】对某电子元件进行寿命追踪调查,所得样本数据的频率分布直方图如下.

(1)求![]() ,并根据图中的数据,用分层抽样的方法抽取
,并根据图中的数据,用分层抽样的方法抽取![]() 个元件,元件寿命落在
个元件,元件寿命落在![]() 之间的应抽取几个?
之间的应抽取几个?
(2)从(1)中抽出的寿命落在![]() 之间的元件中任取
之间的元件中任取![]() 个元件,求事件“恰好有一个元件寿命落在
个元件,求事件“恰好有一个元件寿命落在![]() 之间,一个元件寿命落在
之间,一个元件寿命落在![]() 之间”的概率.
之间”的概率.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)由各矩形面积和为![]() ,求出第二组的面积即频率,根据矩形面积公式可求得
,求出第二组的面积即频率,根据矩形面积公式可求得![]() ,根据前两组的频率可得其在总体中所占比例,乘以样本容量可得寿命落在
,根据前两组的频率可得其在总体中所占比例,乘以样本容量可得寿命落在![]() 之间的元件个数;(2)记“寿命落在
之间的元件个数;(2)记“寿命落在![]() 之间的
之间的![]() 个元件”,分别
个元件”,分别![]() ,“落在
,“落在![]() 之间的
之间的![]() 个元件有”,分别记为:
个元件有”,分别记为:![]() ,从中任取
,从中任取![]() 个元件,列举出所有的基本事件,找出满足条件的基本事件,即可求得概率.
个元件,列举出所有的基本事件,找出满足条件的基本事件,即可求得概率.
试题解析:(1)根据题意:![]() ,解得
,解得![]()
设在寿命落在![]() 之间的应抽取
之间的应抽取![]() 个,根据分层抽样有:
个,根据分层抽样有:![]() 4分
4分
解得:![]() ,所以寿命落在
,所以寿命落在![]() 之间的元件应抽取
之间的元件应抽取![]() 个
个
(2)记“恰好有一个寿命落在![]() 之间,一个寿命为
之间,一个寿命为![]() 之间”为事件
之间”为事件![]() ,易知,寿命落在
,易知,寿命落在![]() 之间的元件有
之间的元件有![]() 个,分别记
个,分别记![]() ,落在
,落在![]() 之间的元件有
之间的元件有![]() 个,分别记为:
个,分别记为:![]() ,从中任取
,从中任取![]() 个元件,有如下基本事件:
个元件,有如下基本事件:
![]()
![]() ,
,![]() ,共有
,共有![]() 个基本事件. 9分
个基本事件. 9分
事件![]() “恰好有一个寿命落在
“恰好有一个寿命落在![]() 之间,一个寿命为
之间,一个寿命为![]() 之间”有:
之间”有:
![]() ,
,![]() ,共有
,共有![]() 个基本事件
个基本事件
∴![]()
∴事件“恰好有一个寿命落在![]() 之间,一个寿命为
之间,一个寿命为![]() 之间”的概率为
之间”的概率为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班的60名同学已编号1,2,3,…,60,为了解该班同学的作业情况,老师收取了号码能被5整除的12名同学的作业本,这里运用的抽样方法是( )
A. 简单随机抽样 B. 系统抽样
C. 分层抽样 D. 抽签法
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
, 是实数,函数
是实数,函数 ,
, ,若
,若 在区间
在区间 上恒成立,则称
上恒成立,则称 和
和 在区间
在区间 上为“
上为“ 函数”.
函数”.(1)设
 ,若
,若 和
和 在区间
在区间 上为“
上为“ 函数”,求实数
函数”,求实数 的取值范围;
的取值范围;(2)设
 ,
,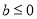 且
且 ,若
,若 和
和 在以
在以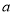 ,
, 为端点的开区间上为“
为端点的开区间上为“ 函数”,求
函数”,求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 .
.(1)当a=2时,判断函数
 在定义域内的单调性;
在定义域内的单调性;(2)当
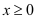 时,
时,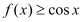 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的左、右焦点分别为
的左、右焦点分别为 ,P为椭圆C上任意一点,且
,P为椭圆C上任意一点,且 最小值为0.
最小值为0.(1)求曲线C的方程;
(2)若动直线
 均与椭圆C相切,且
均与椭圆C相切,且 ,试探究在x轴上是否存在定点B,使得点B到
,试探究在x轴上是否存在定点B,使得点B到 的距离之积恒为1?若存在,请求出点B的坐标;若不存在,请说明理由.
的距离之积恒为1?若存在,请求出点B的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于样本频率分布折线图与总体密度曲线的关系,下列说法中正确的是( )
A. 频率分布折线图与总体密度曲线无关
B. 频率分布折线图就是总体密度曲线
C. 样本容量很大的频率分布折线图就是总体密度曲线
D. 如果样本容量无限增大、分组的组距无限减小,那么频率分布折线图就会无限接近总体密度曲线
-
科目: 来源: 题型:
查看答案和解析>>【题目】将正整数排成下表:
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
……………
则在表中数字2017出现在( )
A. 第44行第80列 B. 第45行第80列 C. 第44行第81列 D. 第45行第81列
相关试题

