【题目】国家放开计划生育政策,鼓励一对夫妇生育2个孩子.在某地区的100000对已经生育了一胎夫妇中,进行大数据统计得,有100对第一胎生育的是双胞胎或多胞胎,其余的均为单胞胎.在这99900对恰好生育一孩的夫妇中,男方、女方都愿意生育二孩的有50000对,男方愿意生育二孩女方不愿意生育二孩的有![]() 对,男方不愿意生育二孩女方愿意生育二孩的有
对,男方不愿意生育二孩女方愿意生育二孩的有![]() 对,其余情形有
对,其余情形有![]() 对,且
对,且![]() .现用样本的频率来估计总体的概率.
.现用样本的频率来估计总体的概率.
(1)说明“其余情形”指何种具体情形,并求出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)该地区为进一步鼓励生育二孩,实行贴补政策:凡第一胎生育了一孩的夫妇一次性贴补5000元,第一胎生育了双胞胎或多胞胎的夫妇只有一次性贴补15000元.第一胎已经生育了一孩再生育了二孩的夫妇一次性再贴补20000元.这种补贴政策直接提高了夫妇生育二孩的积极性:原先男方或女方中只有一方愿意生育二孩的夫妇现在都愿意生育二孩,但原先男方、女方都不愿意生育二孩的夫妇仍然不愿意生育二孩.设![]() 为该地区的一对夫妇享受的生育贴补,求
为该地区的一对夫妇享受的生育贴补,求![]() .
.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据题意中的分类的特点可得“其余情形”的含义,然后利用![]() ,可设
,可设![]() ,由题意求得
,由题意求得![]() 后进而可得所求.(2)由题意得到原先的5种生育情况的频率,由题意可知随机变量
后进而可得所求.(2)由题意得到原先的5种生育情况的频率,由题意可知随机变量![]() 的可能取值为15000,25000,5000,然后求出
的可能取值为15000,25000,5000,然后求出![]() 的每一个取值的概率,从而得到
的每一个取值的概率,从而得到![]() 的分布列,最后可求得期望
的分布列,最后可求得期望![]() .
.
(1)“其余情形”指一对夫妇中的男方、女方都不愿意生育二孩.
由![]() ,可设
,可设![]() ,
,![]() ,
,![]() ,
,
由已知得![]() ,
,
所以![]() ,
,
解得![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
(2)一对夫妇中,原先的生育情况有以下5种:
第一胎生育的是双胞胎或多胞胎有100对,频率为![]() ,
,
男方、女方都愿意生育二孩的有50000对,频率为![]() ,
,
男方愿意生育二胎女方不愿意生育二胎的有30000对,频率为![]() ,
,
男方不愿意生育二胎女方愿意生育二胎的也有10000对,频率为![]() ,
,
其余情形即男方、女方都不愿意生育二孩的有9900对,频率为![]() ,
,
由题意可知随机变量![]() 的可能取值为15000,25000,5000,
的可能取值为15000,25000,5000,
![]() ,
,
![]() ,
,
![]() ,
,
所以随机变量![]() 的概率分布表如下:
的概率分布表如下:
| 15000 | 25000 | 5000 |
|
|
|
|
所以![]() (元).
(元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017高考新课标Ⅲ,理19)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.

(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方体
 中,M,N,E,F分别是棱A1B1,A1D1,B1C1,C1D1的中点,求证:平面AMN∥平面EFDB.
中,M,N,E,F分别是棱A1B1,A1D1,B1C1,C1D1的中点,求证:平面AMN∥平面EFDB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的不等式
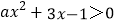 的解集是,
的解集是,
(1)求a的值;
(2)求不等式
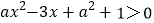 的解集.
的解集. -
科目: 来源: 题型:
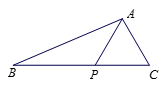
查看答案和解析>>【题目】如图, 在△
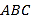 中, 点
中, 点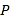 在
在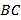 边上,
边上, 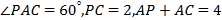 .
.(Ⅰ)求
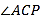 ;
;(Ⅱ)若△
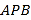 的面积是
的面积是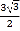 , 求
, 求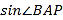 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【题目】已知抛物线C:y2=2x,过点(2,0)的直线l交C于A,B两点,圆M是以线段AB为直径的圆.
(1)证明:坐标原点O在圆M上;
(2)设圆M过点P(4,-2),求直线l与圆M的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 +
+ =1(a>b>0)上的点P到左,右两焦点F1,F2的距离之和为2
=1(a>b>0)上的点P到左,右两焦点F1,F2的距离之和为2 ,离心率为
,离心率为 .
.(1)求椭圆的标准方程;
(2)过右焦点F2的直线l交椭圆于A,B两点,若y轴上一点M(0,
 )满足|MA|=|MB|,求直线l的斜率k的值.
)满足|MA|=|MB|,求直线l的斜率k的值.
相关试题

