【题目】已知圆![]() 与
与![]() 轴负半轴相交于点
轴负半轴相交于点![]() ,与
,与![]() 轴正半轴相交于点
轴正半轴相交于点![]() .
.
(1)若过点 的直线
的直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若在以![]() 为圆心半径为
为圆心半径为![]() 的圆上存在点
的圆上存在点![]() ,使得
,使得![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() 的取值范围;
的取值范围;
(3)设![]() 是圆
是圆![]() 上的两个动点,点
上的两个动点,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,如果直线
,如果直线![]() 与
与![]() 轴分别交于
轴分别交于![]() 和
和![]() ,问
,问![]() 是否为定值?若是求出该定值;若不是,请说明理由.
是否为定值?若是求出该定值;若不是,请说明理由.
参考答案:
【答案】(1)直线![]() 的方程为
的方程为![]() 或
或![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 为定值1..
为定值1..
【解析】试题分析:(1)由题意分类讨论直线的斜率是否存在,根据垂径定理,弦心距,弦长及半径的勾股关系解得k即可求得直线方程;(2) 设点![]() 的坐标为
的坐标为![]() ,由题得点
,由题得点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() 由
由![]() 可得
可得![]() ,化简可得
,化简可得![]() 又点
又点![]() 在圆
在圆![]() 上,所以转化为点p轨迹与圆B有交点即可得解(3)
上,所以转化为点p轨迹与圆B有交点即可得解(3)![]() ,则
,则![]() ,直线
,直线![]() 的方程为
的方程为![]() ,令
,令![]() ,则
,则![]() , 同理可得
, 同理可得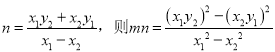 利用
利用![]() 是圆
是圆![]() 上的两个动点即可得定值.
上的两个动点即可得定值.
试题解析:
(1)![]() 若直线
若直线![]() 的斜率不存在,则
的斜率不存在,则![]() 的方程为:
的方程为: ![]() ,符合题意.
,符合题意.
![]() 若直线
若直线![]() 的斜率存在,设
的斜率存在,设![]() 的方程为:
的方程为: ![]() ,即
,即![]()
∴点![]() 到直线
到直线![]() 的距离
的距离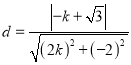
∵直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,∴
,∴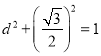
∴![]() ,此时
,此时![]() 的方程为:
的方程为: ![]()
∴所求直线![]() 的方程为
的方程为![]() 或
或![]()
(2)设点![]() 的坐标为
的坐标为![]() ,由题得点
,由题得点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]()
由![]() 可得
可得![]() ,化简可得
,化简可得![]()
∵点![]() 在圆
在圆![]() 上,∴
上,∴![]() ,∴
,∴![]()
∴所求![]() 的取值范围是
的取值范围是![]() .
.
(3)∵![]() ,则
,则![]()
∴直线![]() 的方程为
的方程为![]()
令![]() ,则
,则![]() 同理可得
同理可得![]()
∴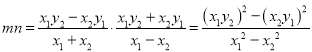

∴![]() 为定值1.
为定值1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)对任意 ,都有xln(kx)﹣kx+1≤mx,求m的取值范围.
,都有xln(kx)﹣kx+1≤mx,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知从椭圆
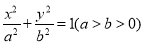 的一个焦点看两短轴端点所成视角为
的一个焦点看两短轴端点所成视角为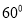 ,且椭圆经过
,且椭圆经过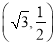 .
.(1)求椭圆的方程;
(2)是否存在实数
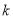 ,使直线
,使直线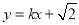 与椭圆有两个不同交点
与椭圆有两个不同交点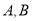 ,且
,且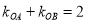 (
(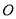 为坐标原点),若存在,求出
为坐标原点),若存在,求出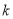 的值.不存在,说明理由.
的值.不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知
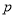 :“直线
:“直线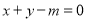 与圆
与圆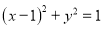 相交”;
相交”; 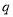 :“
:“ 有一正根和一负根”.若
有一正根和一负根”.若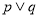 为真,
为真, 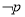 为真,求
为真,求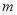 的取值范围.
的取值范围.(2)已知椭圆
 :
: 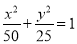 与圆
与圆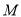 :
:  ,双曲线
,双曲线 与椭圆
与椭圆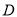 有相同的焦点,它的两条渐近线恰好与圆
有相同的焦点,它的两条渐近线恰好与圆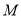 相切.求双曲线
相切.求双曲线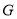 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高三年级进行了一次学业水平测试,用系统抽样的方法抽取了50名学生的数学成绩,准备进行分析和研究.经统计,成绩的分组及各组的频数如下:
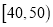 ,2;
,2; 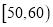 ,3;
,3; 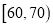 ,10;
,10; 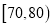
15;
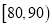 ,12;
,12; 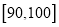 ,8.
,8.(1)完成样本的频率分布表,画出频率分布直方图;
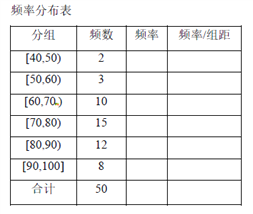
(2)估计成绩在85分以下的学生比例;
(3)请你根据以上信息去估计样本的众数、中位数、平均数(精确到0.01).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
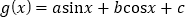 .
.(1)当
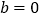 时,求
时,求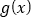 的值域;
的值域;(2)当
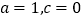 时,函数
时,函数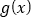 的图象关于
的图象关于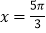 对称,求函数
对称,求函数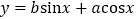 的对称轴.
的对称轴.(3)若
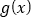 图象上有一个最低点
图象上有一个最低点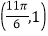 ,如果图象上每点纵坐标不变,横坐标缩短到原来的
,如果图象上每点纵坐标不变,横坐标缩短到原来的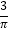 倍,然后向左平移1个单位可得
倍,然后向左平移1个单位可得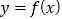 的图象,又知
的图象,又知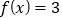 的所有正根从小到大依次为
的所有正根从小到大依次为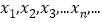 ,且
,且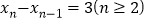 ,求
,求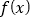 的解析式.
的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
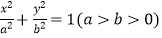 的离心率为
的离心率为 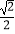 ,右焦点为F,点B(0,1)在椭圆C上.
,右焦点为F,点B(0,1)在椭圆C上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点 的直线交椭圆C于M,N两点,交直线x=2于点P,设
的直线交椭圆C于M,N两点,交直线x=2于点P,设  ,
, 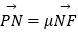 ,求证:λ+μ为定值.
,求证:λ+μ为定值.
相关试题

