【题目】已知从椭圆![]() 的一个焦点看两短轴端点所成视角为
的一个焦点看两短轴端点所成视角为![]() ,且椭圆经过
,且椭圆经过![]() .
.
(1)求椭圆的方程;
(2)是否存在实数![]() ,使直线
,使直线![]() 与椭圆有两个不同交点
与椭圆有两个不同交点![]() ,且
,且![]() (
(![]() 为坐标原点),若存在,求出
为坐标原点),若存在,求出![]() 的值.不存在,说明理由.
的值.不存在,说明理由.
参考答案:
【答案】(1)![]() ;(2)存在,
;(2)存在, ![]() .
.
【解析】试题分析:(1)根据从椭圆![]() 的一个焦点看两短轴端点所成视角为
的一个焦点看两短轴端点所成视角为![]() ,可得
,可得![]() ,由椭圆经过
,由椭圆经过![]() 可得
可得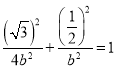 ,联立求解出
,联立求解出![]() 的值即可求椭圆的方程;(2)由
的值即可求椭圆的方程;(2)由 ,根据韦达定理以及经过两点的直线的斜率公式列出关于
,根据韦达定理以及经过两点的直线的斜率公式列出关于![]() 的方程求解即可.
的方程求解即可.
试题解析:(1)由于从椭圆![]() 的一个焦点看两短轴端点所成视角为
的一个焦点看两短轴端点所成视角为![]() ,得,此时,椭圆方程为
,得,此时,椭圆方程为![]() 又因为经过点
又因为经过点![]() ,
,
即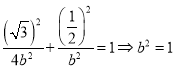 ∴椭圆方程为
∴椭圆方程为![]() .
.
(2)由 ,
,
由![]() 或
或![]() ,设
,设![]() ,则
,则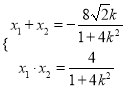
![]() ,
,![]() ,
, ![]()
![]() 即
即![]() ,
, ,
, ![]() 综上可知, 实数
综上可知, 实数![]() 存在且
存在且![]() .
.
【方法点晴】本题主要考查待定系数法求椭圆方程以及直线与椭圆的位置关系和数量积公式,属于难题.用待定系数法求椭圆方程的一般步骤;①作判断:根据条件判断椭圆的焦点在![]() 轴上,还是在
轴上,还是在![]() 轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程
轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程![]() 或
或![]()
![]() ;③找关系:根据已知条件,建立关于
;③找关系:根据已知条件,建立关于![]() 、
、![]() 、
、![]() 的方程组;④得方程:解方程组,将解代入所设方程,即为所求.
的方程组;④得方程:解方程组,将解代入所设方程,即为所求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,平面五边形ABCDE中,AB∥CD,∠BAD=90°,AB=2,CD=1,△ADE是边长为2的正三角形.现将△ADE沿AD折起,得到四棱锥E﹣ABCD(如图2),且DE⊥AB.
(Ⅰ)求证:平面ADE⊥平面ABCD;
(Ⅱ)求平面BCE和平面ADE所成锐二面角的大小;
(Ⅲ)在棱AE上是否存在点F,使得DF∥平面BCE?若存在,求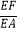 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.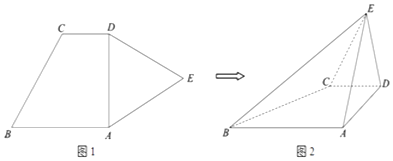
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司购买了A,B,C三种不同品牌的电动智能送风口罩.为了解三种品牌口罩的电池性能,现采用分层抽样的方法,从三种品牌的口罩中抽出25台,测试它们一次完全充电后的连续待机时长,统计结果如下(单位:小时):
A
4
4
4.5
5
5.5
6
6
B
4.5
5
6
6.5
6.5
7
7
7.5
C
5
5
5.5
6
6
7
7
7.5
8
8
(1)已知该公司购买的C品牌电动智能送风口罩比B品牌多200台,求该公司购买的B品牌电动智能送风口罩的数量;
(2)从A品牌和B品牌抽出的电动智能送风口罩中,各随机选取一台,求A品牌待机时长高于B品牌的概率;
(3)再从A,B,C三种不同品牌的电动智能送风口罩中各随机抽取一台,它们的待机时长分别是a,b,c(单位:小时).这3个新数据与表格中的数据构成的新样本的平均数记为μ1 , 表格中数据的平均数记为μ0 . 若μ0≤μ1 , 写出a+b+c的最小值(结论不要求证明). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)对任意 ,都有xln(kx)﹣kx+1≤mx,求m的取值范围.
,都有xln(kx)﹣kx+1≤mx,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知
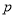 :“直线
:“直线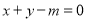 与圆
与圆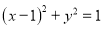 相交”;
相交”; 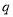 :“
:“ 有一正根和一负根”.若
有一正根和一负根”.若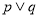 为真,
为真, 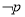 为真,求
为真,求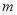 的取值范围.
的取值范围.(2)已知椭圆
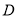 :
: 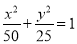 与圆
与圆 :
:  ,双曲线
,双曲线 与椭圆
与椭圆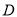 有相同的焦点,它的两条渐近线恰好与圆
有相同的焦点,它的两条渐近线恰好与圆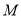 相切.求双曲线
相切.求双曲线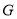 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 与
与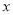 轴负半轴相交于点
轴负半轴相交于点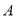 ,与
,与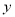 轴正半轴相交于点
轴正半轴相交于点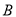 .
.(1)若过点
 的直线
的直线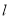 被圆
被圆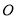 截得的弦长为
截得的弦长为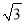 ,求直线
,求直线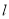 的方程;
的方程;(2)若在以
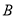 为圆心半径为
为圆心半径为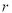 的圆上存在点
的圆上存在点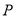 ,使得
,使得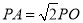 (
(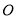 为坐标原点),求
为坐标原点),求 的取值范围;
的取值范围;(3)设
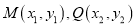 是圆
是圆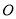 上的两个动点,点
上的两个动点,点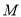 关于原点的对称点为
关于原点的对称点为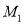 ,点
,点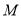 关于
关于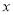 轴的对称点为
轴的对称点为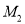 ,如果直线
,如果直线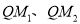 与
与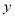 轴分别交于
轴分别交于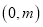 和
和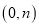 ,问
,问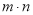 是否为定值?若是求出该定值;若不是,请说明理由.
是否为定值?若是求出该定值;若不是,请说明理由. -
科目: 来源: 题型:
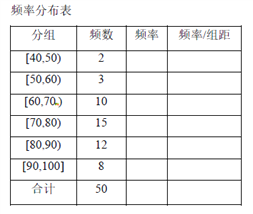
查看答案和解析>>【题目】某校高三年级进行了一次学业水平测试,用系统抽样的方法抽取了50名学生的数学成绩,准备进行分析和研究.经统计,成绩的分组及各组的频数如下:
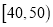 ,2;
,2; 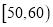 ,3;
,3; 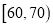 ,10;
,10; 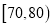
15;
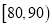 ,12;
,12;  ,8.
,8.(1)完成样本的频率分布表,画出频率分布直方图;
(2)估计成绩在85分以下的学生比例;
(3)请你根据以上信息去估计样本的众数、中位数、平均数(精确到0.01).
相关试题

