【题目】已知函数![]() 有两个不同的极值点
有两个不同的极值点![]() ,
,![]() ,且
,且![]() .
.
(1)求实数![]() 的取值范围;
的取值范围;
(2)设上述![]() 的取值范围为
的取值范围为![]() ,若存在
,若存在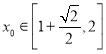 ,使对任意
,使对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)注意函数![]() 的定义域,对函数
的定义域,对函数![]() 求导,令
求导,令![]() ,则
,则![]() ,根据方程有两个不等正根,求出
,根据方程有两个不等正根,求出![]() 的范围;(2)求出函数
的范围;(2)求出函数![]() 在
在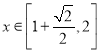 上的单调性,并求出最大值,已知恒成立转化为
上的单调性,并求出最大值,已知恒成立转化为![]() 恒成立,设
恒成立,设![]() ,则
,则![]() 的最小值大于
的最小值大于![]() 即可,讨论函数
即可,讨论函数![]() 的单调性,求出
的单调性,求出![]() 的范围.
的范围.
试题解析:(1)![]() ,
,
令![]() ,则
,则![]() ,
,
根据题意,方程有两个不等正根,则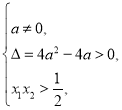 即
即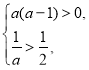
解得![]() ,
,
故实数![]() 的取值范围是
的取值范围是![]() .
.
(2)由![]() ,得
,得![]() .
.
即![]() 或
或![]() ,
,
所以![]() 在
在![]() 和
和![]() 上是增函数,
上是增函数,
因为![]() ,则
,则![]() ,所以
,所以![]() 在
在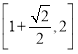 上是增函数,
上是增函数,
当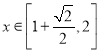 时,
时,
![]() .
.
由题意,当![]() 时,
时,![]() 恒成立,即
恒成立,即
![]() ,即
,即![]() 恒成立,
恒成立,
设![]() ,
,
则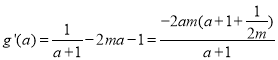 .
.
(1)当![]() 时,因为
时,因为![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上是减函数,
上是减函数,
此时,![]() ,不合题意.
,不合题意.
(2)当![]() 时,若
时,若![]() ,即
,即![]() ,因为
,因为![]() ,则
,则![]() ,
,![]() ,
,
所以![]() 在
在![]() 上是增函数,此时
上是增函数,此时![]() ,符合题意.
,符合题意.
若![]() ,即
,即![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上是减函数,
上是减函数,
此时,![]() ,不合题意.
,不合题意.
综上可知,![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家外卖公司,其送餐员的日工资方案如下:甲公司的底薪80元,每单抽成4元;乙公司无底薪,40单以内(含40单)的部分每单抽成6元,超出40单的部分每单抽成7元,假设同一公司送餐员一天的送餐单数相同,现从两家公司各随机抽取一名送餐员,并分别记录其50天的送餐单数,得到如下频数表:
甲公司送餐员送餐单数频数表
送餐单数
38
39
40
41
42
天数
10
15
10
10
5
乙公司送餐员送餐单数频数表
送餐单数
38
39
40
41
42
天数
5
10
10
20
5
(1)现从甲公司记录的50天中随机抽取3天,求这3天送餐单数都不小于40的概率;
(2)若将频率视为概率,回答下列两个问题:
①记乙公司送餐员日工资为
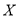 (单位:元),求
(单位:元),求 的分布列和数学期望;
的分布列和数学期望;②小王打算到甲、乙两家公司中的一家应聘送餐员,如果仅从日工资的角度考虑,请利用所学的统计学知识为小王作出选择,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在棱锥
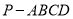 中,
中, 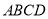 为矩形,
为矩形,  面
面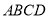 ,
, 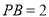 ,
, 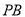 与面
与面 成
成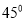 角,
角, 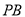 与面
与面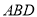 成
成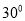 角.
角. (1)在
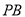 上是否存在一点
上是否存在一点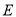 ,使
,使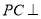 面
面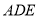 ,若存在确定
,若存在确定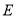 点位置,若不存在,请说明理由;
点位置,若不存在,请说明理由;(2)当
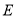 为
为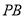 中点时,求二面角
中点时,求二面角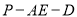 的余弦值.
的余弦值. 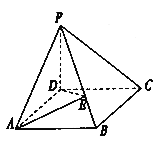
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:  的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切.  、
、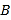 是椭圆
是椭圆 的右顶点与上顶点,直线
的右顶点与上顶点,直线 与椭圆相交于
与椭圆相交于 、
、 两点.
两点.
(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)当四边形
 面积取最大值时,求
面积取最大值时,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某次有600人参加的数学测试,其成绩的频数分布表如图所示,规定85分及其以上为优秀.
区间
[75,80)
[80,85)
[85,90)
[90,95)
[95,100]
人数
36
114
244
156
50
(Ⅰ)现用分层抽样的方法从这600人中抽取20人进行成绩分析,求其中成绩为优秀的学生人数;
(Ⅱ)在(Ⅰ)中抽取的20名学生中,要随机选取2名学生参加活动,记“其中成绩为优秀的人数”为
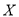 ,求
,求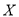 的分布列与数学期望.
的分布列与数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱柱
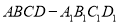 中,
中, 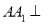 平面
平面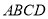 ,底面
,底面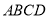 为梯形,
为梯形, 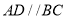 ,
, 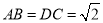 ,
, 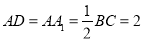 ,点
,点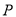 ,
, 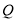 分别为
分别为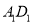 ,
, 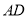 的中点.
的中点. 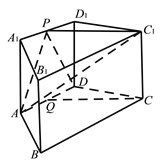
(Ⅰ)求证:
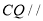 平面
平面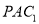 ;
; (Ⅱ)求二面角
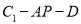 的余弦值;
的余弦值; (Ⅲ)在线段
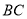 上是否存在点
上是否存在点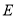 ,使
,使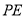 与平面
与平面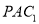 所成角的正弦值是
所成角的正弦值是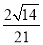 ,若存在,求
,若存在,求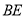 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

 .
.(Ⅰ)当
 时,求函数
时,求函数 的单调区间;
的单调区间;(Ⅱ)对任意的
 ,
,  恒成立,求
恒成立,求 的取值范围.
的取值范围.
相关试题

