【题目】如图,在四棱柱![]() 中,
中, ![]() 平面
平面![]() ,底面
,底面![]() 为梯形,
为梯形, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.
的中点.
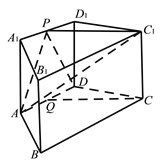
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 与平面
与平面![]() 所成角的正弦值是
所成角的正弦值是![]() ,若存在,求
,若存在,求![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
参考答案:
【答案】(Ⅰ)见解析;(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】试题分析:(Ⅰ)连接![]() ,证明四边形
,证明四边形![]() 是平行四边形. 得到
是平行四边形. 得到![]() ,即可证明
,即可证明![]() 平面
平面![]()
(Ⅱ)以![]() 为坐标原点,分别以直线
为坐标原点,分别以直线![]() ,
, ![]() 为
为![]() 轴,
轴, ![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,分别求出面
,分别求出面![]() 的法向量
的法向量![]() 和面
和面![]() 的法向量
的法向量![]() ,即可求出二面角
,即可求出二面角![]() 的余弦值;
的余弦值;
(Ⅲ)存设点![]() ,所以
,所以![]()
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,所以
,所以![]()
所以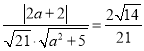 ,即可求出
,即可求出![]() 的长
的长
试题解析:(Ⅰ)连接![]() ,因为点
,因为点![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,
的中点,
所以![]() ,
, ![]() .
.
所以四边形![]() 是平行四边形.
是平行四边形.
所以![]()
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]()
(Ⅱ)因为![]() 平面
平面![]() ,
, ![]() ,
,
所以![]() 平面
平面![]() .
.
所以以![]() 为坐标原点,分别以直线
为坐标原点,分别以直线![]() ,
, ![]() 为
为![]() 轴,
轴, ![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,则
,则![]() 轴在平面
轴在平面![]() 内.
内.
所以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以![]() ,
, ![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,所以
,所以 即
即![]()
所以![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
所以![]()
又二面角![]() 为锐角,
为锐角,
所以二面角![]() 的余弦值是
的余弦值是![]()
(Ⅲ)存在. 设点![]() ,所以
,所以![]()
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,所以
,所以![]()
所以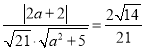 ,解得
,解得![]()
所以![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:  的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切.  、
、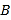 是椭圆
是椭圆 的右顶点与上顶点,直线
的右顶点与上顶点,直线 与椭圆相交于
与椭圆相交于 、
、 两点.
两点.
(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)当四边形
 面积取最大值时,求
面积取最大值时,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
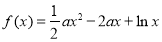 有两个不同的极值点
有两个不同的极值点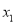 ,
,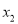 ,且
,且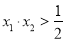 .
.(1)求实数
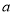 的取值范围;
的取值范围;(2)设上述
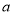 的取值范围为
的取值范围为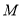 ,若存在
,若存在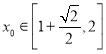 ,使对任意
,使对任意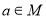 ,不等式
,不等式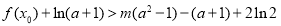 恒成立,求实数
恒成立,求实数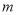 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某次有600人参加的数学测试,其成绩的频数分布表如图所示,规定85分及其以上为优秀.
区间
[75,80)
[80,85)
[85,90)
[90,95)
[95,100]
人数
36
114
244
156
50
(Ⅰ)现用分层抽样的方法从这600人中抽取20人进行成绩分析,求其中成绩为优秀的学生人数;
(Ⅱ)在(Ⅰ)中抽取的20名学生中,要随机选取2名学生参加活动,记“其中成绩为优秀的人数”为
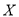 ,求
,求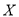 的分布列与数学期望.
的分布列与数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

 .
.(Ⅰ)当
 时,求函数
时,求函数 的单调区间;
的单调区间;(Ⅱ)对任意的
 ,
,  恒成立,求
恒成立,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
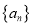 的首项为
的首项为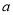 ,公差为
,公差为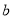 ,等比数列
,等比数列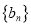 的首项为
的首项为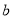 ,公比为
,公比为 .
. (Ⅰ)若数列
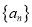 的前
的前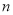 项和
项和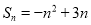 ,求
,求 ,
, 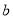 的值;
的值;(Ⅱ)若
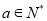 ,
, 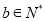 ,且
,且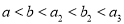 .
. (i)求
 的值;
的值;(ii)对于数列
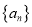 和
和 ,满足关系式
,满足关系式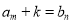 ,
, 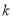 为常数,且
为常数,且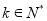 ,求
,求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为了准确把握市场,做好产品计划,特对某产品做了市场调查:先销售该产品50天,统计发现每天的销售量
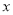 分布在
分布在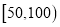 内,且销售量
内,且销售量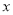 的分布频率
的分布频率 .
.(Ⅰ)求
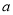 的值并估计销售量的平均数;
的值并估计销售量的平均数;(Ⅱ)若销售量大于等于70,则称该日畅销,其余为滞销.在畅销日中用分层抽样的方法随机抽取8天,再从这8天中随机抽取3天进行统计,设这3天来自
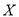 个组,求随机变量
个组,求随机变量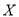 的分布列及数学期望(将频率视为概率).
的分布列及数学期望(将频率视为概率).
相关试题

