11. (1)求涂色部分的周长。
(2)求涂色部分的面积。

 ]
]
(2)求涂色部分的面积。

 ]
]
答案:
11.
(1)3.14×10+20×2=71.4(cm)
(2)8÷2=4(m) 3.14×4²÷2−4×4÷2=17.12(m²)
(1)3.14×10+20×2=71.4(cm)
(2)8÷2=4(m) 3.14×4²÷2−4×4÷2=17.12(m²)
12. 一辆自行车轮胎的外直径约为1m。如果平均每分钟转动100周,那么它5分钟能前进多少米?
答案:
12.3.14×1×100×5=1570(m)
13. 如图,一个半圆形的菜地靠墙而建,半径为6m。
(1)要给这个菜地围上围栏,需要多长的围栏?

(2)为了方便行走,在这个菜地外面,沿着围栏铺一条宽1m的小路,请在上图中画出示意图,标上数据,并计算小路的面积是多少。
(1)要给这个菜地围上围栏,需要多长的围栏?

(2)为了方便行走,在这个菜地外面,沿着围栏铺一条宽1m的小路,请在上图中画出示意图,标上数据,并计算小路的面积是多少。
答案:
1. (1)
解:求围栏长度,即求半圆的弧长。
根据圆的周长公式$C = 2\pi r$($r$为半径),半圆的弧长$l=\frac{1}{2}×2\pi r=\pi r$。
已知$r = 6m$,$\pi$取$3.14$,则$l = 3.14×6=18.84m$。
2. (2)
首先画示意图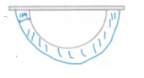 。
。
解:求小路面积,即求半圆环的面积。
外圆半径$R=r + 1=6 + 1=7m$,内圆半径$r = 6m$。
根据圆环面积公式$S=\pi(R^{2}-r^{2})$,半圆环面积$S_{半}=\frac{1}{2}\pi(R^{2}-r^{2})$。
把$R = 7m$,$r = 6m$,$\pi = 3.14$代入可得:
$S_{半}=\frac{1}{2}×3.14×(7^{2}-6^{2})$
先计算$7^{2}-6^{2}=(7 + 6)(7 - 6)=13$。
则$S_{半}=\frac{1}{2}×3.14×13=20.41m^{2}$。
综上,(1)需要$18.84m$长的围栏;(2)小路的面积是$20.41m^{2}$。
1. (1)
解:求围栏长度,即求半圆的弧长。
根据圆的周长公式$C = 2\pi r$($r$为半径),半圆的弧长$l=\frac{1}{2}×2\pi r=\pi r$。
已知$r = 6m$,$\pi$取$3.14$,则$l = 3.14×6=18.84m$。
2. (2)
首先画示意图
 。
。解:求小路面积,即求半圆环的面积。
外圆半径$R=r + 1=6 + 1=7m$,内圆半径$r = 6m$。
根据圆环面积公式$S=\pi(R^{2}-r^{2})$,半圆环面积$S_{半}=\frac{1}{2}\pi(R^{2}-r^{2})$。
把$R = 7m$,$r = 6m$,$\pi = 3.14$代入可得:
$S_{半}=\frac{1}{2}×3.14×(7^{2}-6^{2})$
先计算$7^{2}-6^{2}=(7 + 6)(7 - 6)=13$。
则$S_{半}=\frac{1}{2}×3.14×13=20.41m^{2}$。
综上,(1)需要$18.84m$长的围栏;(2)小路的面积是$20.41m^{2}$。
14. 妈妈带东东去吃比萨,点了一个直径是30cm的圆形比萨,但是服务员说30cm的比萨已经卖完,换成2个直径是20cm的同款比萨给东东。服务员说这是多送了比萨给东东,东东却对妈妈说:“没有多送,反而少了。”东东说得对不对? 请你用学过的知识通过列式计算来说明。
答案:
14.东东说得对。3.14×(30÷2)²=706.5(cm²) 3.14×(20÷2)²×2=628(cm²) 706.5>628,所以没有多送,反而少了
查看更多完整答案,请扫码查看


