《2025年天星教育试题调研物理第10辑》

调研19 试题调研原创 如图所示,带有阀门的导热

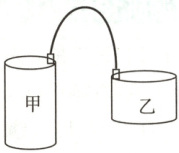
储

气罐甲、乙中装有同种气体(可视为理想气体)，开始时阀门关闭，甲罐的体积为$V_0$，罐中气体的质量为$m$，在温度为$27° C$时，甲、乙中气体的压强分别为$3p_0$和$p_0$，现用甲罐通过细导气管(体积可忽略)对乙罐充气，充气时甲罐在$27° C$的室温中，把乙罐放在$-13° C$的环境中。充气完毕稳定后，关闭阀门，撤去导气管，测得乙罐中的气体在温度为$27° C$时的压强达到$2.5p_0$。充气过程中甲、乙罐中的气体温度始终分别与各自外界相等，各处气密性良好，已知$T=t + 273K$。求：
(1)乙罐的体积。
(2)充气完毕后，甲、乙罐中气体的质量之比。

 

答案：
(1)设乙罐的体积为$V$。充气完毕稳定后，甲、乙罐中气体压强均为$p_1$，乙罐气体温度$T_2=260K$（$-13^{\circ}C$），甲罐气体温度$T_1=300K$（$27^{\circ}C$）。关闭阀门后，乙罐气体温度升至$T_1=300K$时压强为$2.5p_0$，由查理定律得：
$\frac{p_1}{T_2}=\frac{2.5p_0}{T_1}$
代入$T_1=300K$，$T_2=260K$，解得$p_1=\frac{13}{6}p_0$。
充气过程中，甲、乙气体总质量守恒，由理想气体状态方程：
$\frac{3p_0V_0}{T_1}+\frac{p_0V}{T_1}=\frac{p_1V_0}{T_1}+\frac{p_1V}{T_2}$
代入$p_1=\frac{13}{6}p_0$，$T_1=300K$，$T_2=260K$，解得$V=\frac{5}{9}V_0$。
(2)充气完毕后，甲罐气体：$p=p_1$，$V=V_0$，$T=T_1$；乙罐气体：$p=p_1$，$V=\frac{5}{9}V_0$，$T=T_2$。由$m=\frac{pVM}{RT}$，质量之比：
$\frac{m_甲}{m_乙}=\frac{V_0T_2}{VT_1}$
代入$V=\frac{5}{9}V_0$，$T_1=300K$，$T_2=260K$，解得$\frac{m_甲}{m_乙}=\frac{39}{25}$。
(1)$\frac{5}{9}V_0$
(2)$\frac{39}{25}$