《2025年一线名师权威试卷统考模拟卷六年级数学上册人教版》

3. 甲数的 50%等于乙数的$\dfrac{1}{4}$(甲、乙均不为 0),则甲数(A)乙数。
A.小于
B.等于
C.大于
D.无法判断

答案： [A]

4. 有三根同样长的铁丝,每根铁丝首尾相连,分别围成一个长方形、正方形和圆,它们的面积相比,(B)的面积最小。
A.正方形
B.长方形
C.圆
D.无法确定

答案： [B]

5. 一杯牛奶喝了 60%后,还剩 90g,这杯牛奶原有(D)g。
A.54
B.144
C.150
D.225

答案： [D]

6. 一件衣服降价 20 元,现价是 80 元,降价幅度是(B)。
A.25%
B.20%
C.15%
D.10%

答案： [B]

三、求出下列图形中阴影部分的面积。(12 分)

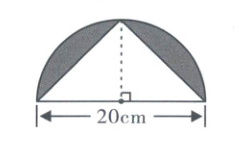
答案： 第一个图形
- **分析**：
阴影部分面积$S = $半圆面积$-$三角形面积。
已知半圆直径$d = 20cm$，则半径$r=\frac{d}{2}=10cm$，三角形的底为$20cm$，高为$10cm$。
半圆面积公式$S_{半圆}=\frac{1}{2}\pi r^{2}$，三角形面积公式$S_{\triangle}=\frac{1}{2}ah$（$a$为底，$h$为高）。
计算**：
$S_{半圆}=\frac{1}{2}×3.14×10^{2}=157cm^{2}$。
$S_{\triangle}=\frac{1}{2}×20×10 = 100cm^{2}$。
$S = 157-100=57cm^{2}$。
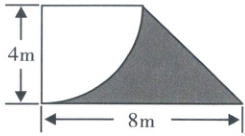
第二个图形
- **分析**：
阴影部分面积$S=$梯形面积$-\frac{1}{4}$圆面积。
梯形的上底$a = 4m$，下底$b = 8m$，高$h = 4m$，圆半径$r = 4m$。
梯形面积公式$S_{梯}=\frac{(a + b)h}{2}$，圆面积公式$S_{圆}=\pi r^{2}$。
计算**：
$S_{梯}=\frac{(4 + 8)×4}{2}=24m^{2}$。
$S_{\frac{1}{4}圆}=\frac{1}{4}×3.14×4^{2}=12.56m^{2}$。
$S = 24-12.56 = 11.44m^{2}$。
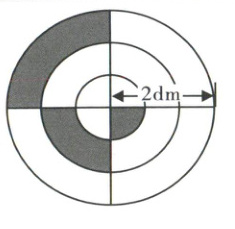
第三个图形
- **分析**：
把阴影部分通过旋转、平移等方法可拼成$\frac{1}{4}$圆环。
外圆半径$R = 2×3 = 6dm$，内圆半径$r = 2×2 = 4dm$，$r_{1}=2dm$。
圆环面积公式$S_{环}=\pi(R^{2}-r^{2})$。
计算**：
$S=\frac{1}{4}×3.14×(6^{2}-4^{2}+2^{2}-0^{2})$
$=\frac{1}{4}×3.14×(36 - 16+4)$
$=\frac{1}{4}×3.14×24=18.84dm^{2}$。
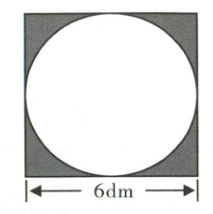
第四个图形
- **分析**：
阴影部分面积$S=$正方形面积$-$圆面积。
正方形边长$a = 6dm$，圆半径$r=\frac{6}{2}=3dm$。
正方形面积公式$S_{正}=a^{2}$，圆面积公式$S_{圆}=\pi r^{2}$。
计算**：
$S_{正}=6×6 = 36dm^{2}$。
$S_{圆}=3.14×3^{2}=28.26dm^{2}$。
$S = 36-28.26=7.74dm^{2}$。
综上，四个图形阴影部分面积分别为$\boldsymbol{57cm^{2}}$、$\boldsymbol{11.44m^{2}}$、$\boldsymbol{18.84dm^{2}}$、$\boldsymbol{7.74dm^{2}}$。