《2025年单元自测试卷青岛出版社六年级数学上册人教版》

4. 一捆铁丝长31.4米,在一根圆柱形铁棒上正好绕了200圈。这根铁棒的横截面半径是多少厘米?

答案： 4.2.5厘米

5. 去年一场大雪过后,地上白茫茫一片,但学校花坛周围小路上的雪被同学们打扫得干干净净(如下图)。小路的面积是多少?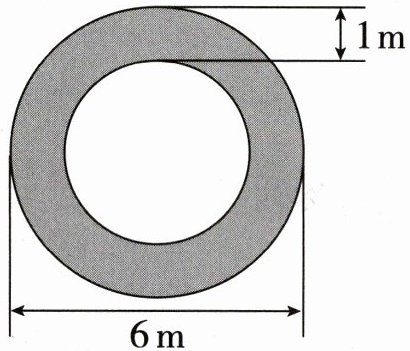

答案： 5.15.7平方米

6. 一段篱笆长18.84米,如果用这段篱笆围成一个最大的圆形羊圈,那么这个羊圈的面积是多少平方米?

答案： 6.28.26平方米

1. 一种童车前轮直径是0.28米,后轮直径是0.35米。当该车前轮行走20圈的路程时,后轮转动了多少圈?

答案： 1.16圈

2. 正方形内有一个最大的圆,已知正方形的面积是100 $cm^2$,求圆的面积。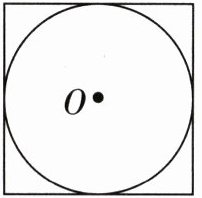

答案： 1. 首先求正方形的边长：
设正方形的边长为$a$，根据正方形面积公式$S = a^{2}$，已知$S = 100cm^{2}$，则$a=\sqrt{100}=10cm$。
2. 然后分析圆与正方形的关系：
因为正方形内最大圆的直径$d$等于正方形的边长$a$，所以$d = 10cm$，那么圆的半径$r=\frac{d}{2}=\frac{10}{2}=5cm$。
3. 最后求圆的面积：
根据圆的面积公式$S=\pi r^{2}$（$\pi$取$3.14$），将$r = 5cm$代入公式，可得$S = 3.14×5^{2}$。
计算$3.14×5^{2}=3.14×25 = 78.5cm^{2}$。
答：圆的面积是$78.5cm^{2}$。