第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 要判断一个角是锐角还是钝角,可以用三角尺上的(
直
)角比一比。
答案:
直
2. 根据角的大小我们把角分为(
三
)类:一类是直角;比直角小的角,我们把它叫作(锐
)角;比直角大的角,叫作(钝
)角。
答案:
三 锐 钝
3. 三角尺上有(
三
)个角,其中一定有一个角是(直
)角,两个角是(锐
)角。
答案:
三 直 锐
二、下面钟面上的时针和分针形成的角分别是什么角?

锐角都比直角(
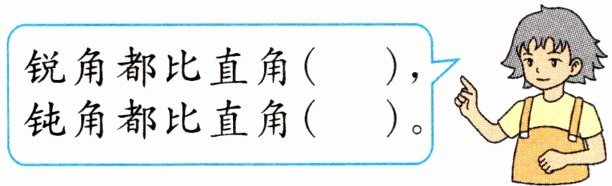
三种角的大小关系:
(

锐角都比直角(
小
),钝角都比直角(大
)。
三种角的大小关系:
(
锐
)角<(直
)角<(钝
)角。
答案:
钝 直 锐 钝 小 大 锐 直 钝
三、找一找,填一填。
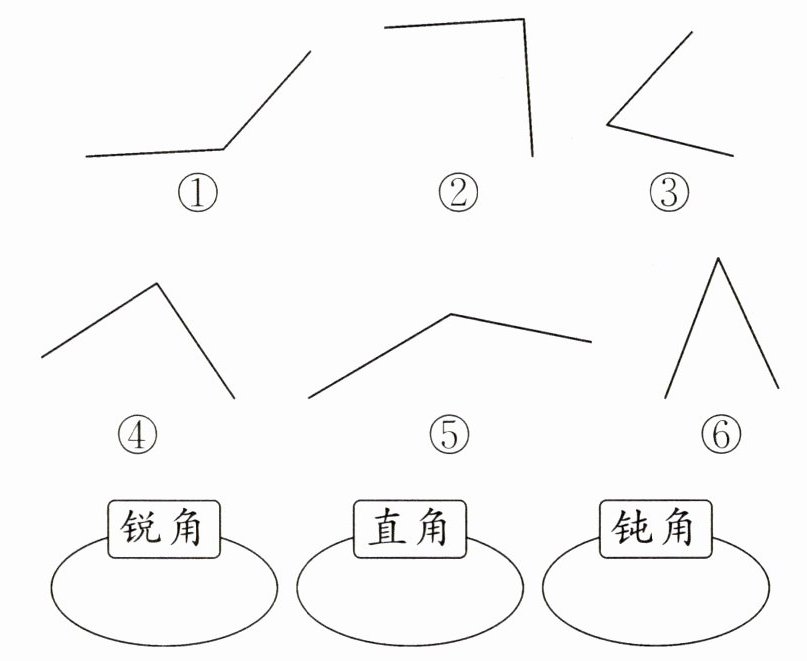

③⑥ ②④ ①⑤
答案:
③⑥ ②④ ①⑤
四、找出下面三角形中的直角、锐角和钝角。你有什么发现?
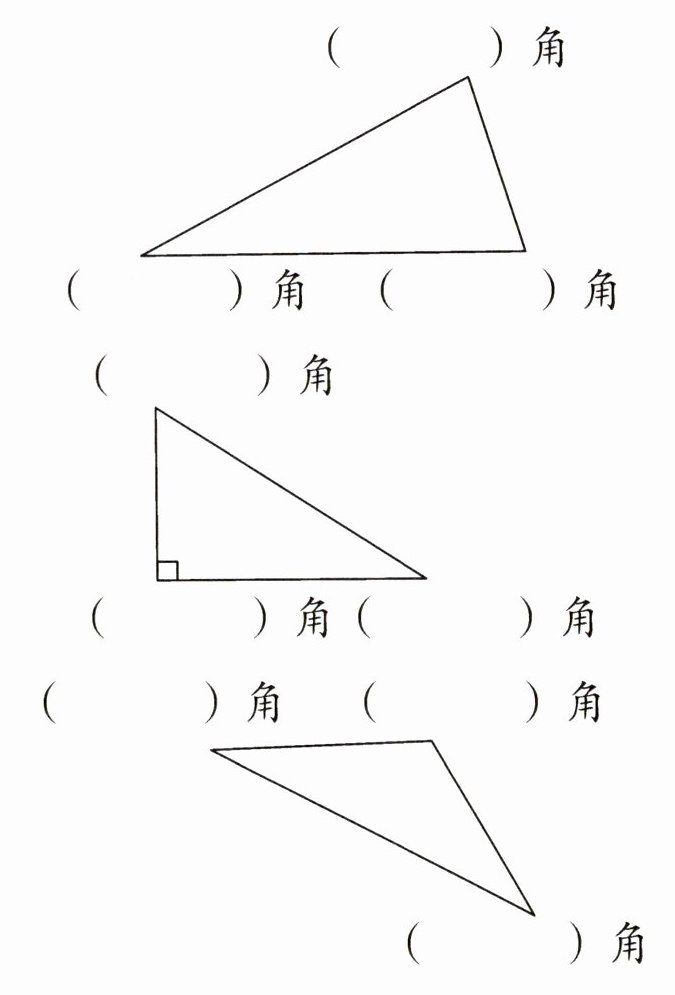
我发现:一个三角形中最少有(

我发现:一个三角形中最少有(
2
)个锐角,最多有(1
)个直角或钝角。
答案:
1. 首先明确角的分类:
锐角:大于$0^{\circ}$而小于$90^{\circ}$的角;直角:等于$90^{\circ}$的角;钝角:大于$90^{\circ}$而小于$180^{\circ}$的角。
2. 然后判断第一个三角形:
三个角分别为(锐)角、(锐)角、(锐)角(因为三个角都小于$90^{\circ}$)。
3. 接着判断第二个三角形:
三个角分别为(直)角、(锐)角、(锐)角。
4. 最后判断第三个三角形:
三个角分别为(钝)角、(锐)角、(锐)角。
5. 总结发现:
因为三角形内角和为$180^{\circ}$,如果只有$1$个锐角,那么另外两个角的和就会大于$90^{\circ}$,若这两个角中有一个直角($90^{\circ}$)或钝角(大于$90^{\circ}$),就不满足三角形内角和是$180^{\circ}$了。所以一个三角形中最少有$2$个锐角;又因为如果有$2$个或$3$个直角或钝角,内角和就会大于$180^{\circ}$,所以最多有$1$个直角或钝角。
故答案依次为:$2$;$1$。
锐角:大于$0^{\circ}$而小于$90^{\circ}$的角;直角:等于$90^{\circ}$的角;钝角:大于$90^{\circ}$而小于$180^{\circ}$的角。
2. 然后判断第一个三角形:
三个角分别为(锐)角、(锐)角、(锐)角(因为三个角都小于$90^{\circ}$)。
3. 接着判断第二个三角形:
三个角分别为(直)角、(锐)角、(锐)角。
4. 最后判断第三个三角形:
三个角分别为(钝)角、(锐)角、(锐)角。
5. 总结发现:
因为三角形内角和为$180^{\circ}$,如果只有$1$个锐角,那么另外两个角的和就会大于$90^{\circ}$,若这两个角中有一个直角($90^{\circ}$)或钝角(大于$90^{\circ}$),就不满足三角形内角和是$180^{\circ}$了。所以一个三角形中最少有$2$个锐角;又因为如果有$2$个或$3$个直角或钝角,内角和就会大于$180^{\circ}$,所以最多有$1$个直角或钝角。
故答案依次为:$2$;$1$。
查看更多完整答案,请扫码查看


