第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
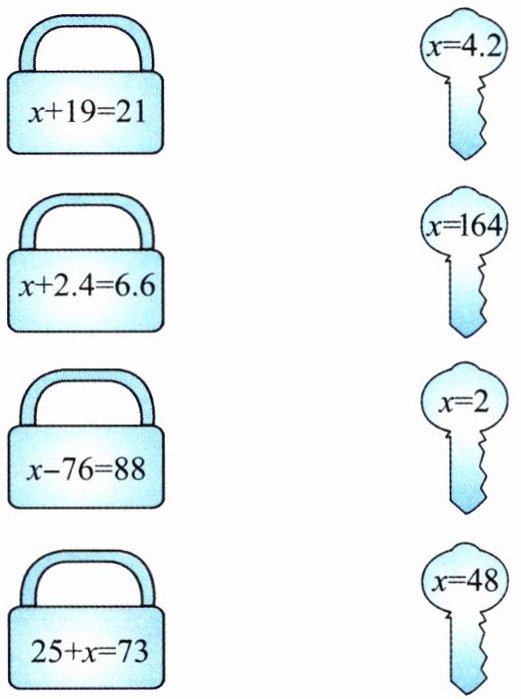
1. 填一填,解方程。
(1) $ x + 0.5 = 2.5 $
解:$ x + 0.5 - 0.5 = 2.5 $
$ x = $
(2) $ x - 18 = 54 $
解:$ x - 18 + $
$ x = $
(1) $ x + 0.5 = 2.5 $
解:$ x + 0.5 - 0.5 = 2.5 $
-
0.5
$ x = $
2
(2) $ x - 18 = 54 $
解:$ x - 18 + $
18
$ = 54 $+
18
$ x = $
72

答案:
1.
(1)- 0.5 2
(2)18 + 18 72
(1)- 0.5 2
(2)18 + 18 72
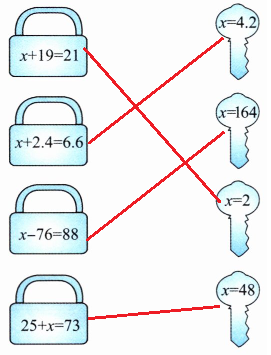
2. 连一连。
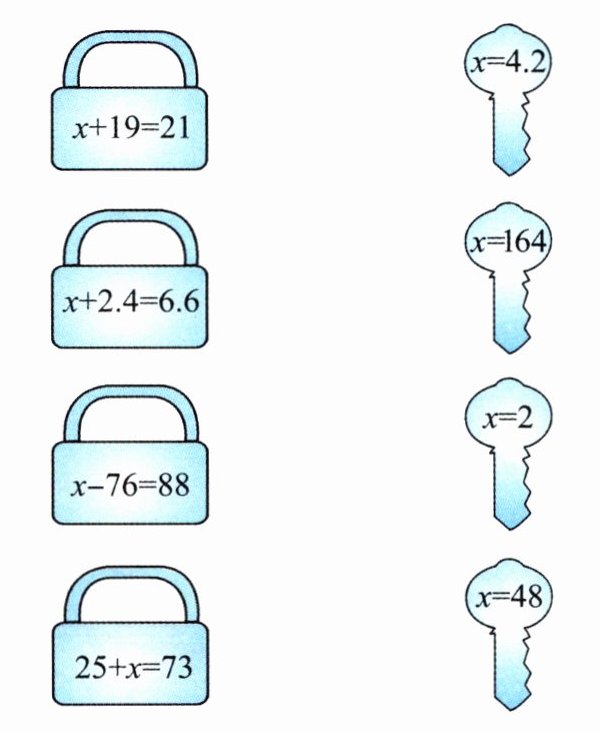

答案:

3. 解下列方程并检验。
$ 7.6 + x = 34.5 $ $ x - 74 = 102 $
$ x + 2.4 = 8 $ $ x - 4.2 = 3.6 $
$ 7.6 + x = 34.5 $ $ x - 74 = 102 $
$ x + 2.4 = 8 $ $ x - 4.2 = 3.6 $
答案:
解方程$7.6 + x = 34.5$
解:根据等式的性质,等式两边同时减去一个数,等式仍然成立。
在方程$7.6 + x = 34.5$两边同时减去$7.6$,可得:
$x=34.5 - 7.6$
$x = 26.9$
检验:
把$x = 26.9$代入原方程左边$=7.6+26.9 = 34.5$,右边$ = 34.5$,
因为左边$=$右边,所以$x = 26.9$是原方程的解。
解方程$x - 74 = 102$
解:根据等式的性质,等式两边同时加上一个数,等式仍然成立。
在方程$x - 74 = 102$两边同时加上$74$,可得:
$x=102 + 74$
$x = 176$
检验:
把$x = 176$代入原方程左边$=176-74 = 102$,右边$ = 102$,
因为左边$=$右边,所以$x = 176$是原方程的解。
解方程$x + 2.4 = 8$
解:根据等式的性质,等式两边同时减去一个数,等式仍然成立。
在方程$x + 2.4 = 8$两边同时减去$2.4$,可得:
$x=8 - 2.4$
$x = 5.6$
检验:
把$x = 5.6$代入原方程左边$=5.6+2.4 = 8$,右边$ = 8$,
因为左边$=$右边,所以$x = 5.6$是原方程的解。
解方程$x - 4.2 = 3.6$
解:根据等式的性质,等式两边同时加上一个数,等式仍然成立。
在方程$x - 4.2 = 3.6$两边同时加上$4.2$,可得:
$x=3.6 + 4.2$
$x = 7.8$
检验:
把$x = 7.8$代入原方程左边$=7.8-4.2 = 3.6$,右边$ = 3.6$,
因为左边$=$右边,所以$x = 7.8$是原方程的解。
综上,方程$7.6 + x = 34.5$的解为$x = 26.9$;方程$x - 74 = 102$的解为$x = 176$;方程$x + 2.4 = 8$的解为$x = 5.6$;方程$x - 4.2 = 3.6$的解为$x = 7.8$。
解:根据等式的性质,等式两边同时减去一个数,等式仍然成立。
在方程$7.6 + x = 34.5$两边同时减去$7.6$,可得:
$x=34.5 - 7.6$
$x = 26.9$
检验:
把$x = 26.9$代入原方程左边$=7.6+26.9 = 34.5$,右边$ = 34.5$,
因为左边$=$右边,所以$x = 26.9$是原方程的解。
解方程$x - 74 = 102$
解:根据等式的性质,等式两边同时加上一个数,等式仍然成立。
在方程$x - 74 = 102$两边同时加上$74$,可得:
$x=102 + 74$
$x = 176$
检验:
把$x = 176$代入原方程左边$=176-74 = 102$,右边$ = 102$,
因为左边$=$右边,所以$x = 176$是原方程的解。
解方程$x + 2.4 = 8$
解:根据等式的性质,等式两边同时减去一个数,等式仍然成立。
在方程$x + 2.4 = 8$两边同时减去$2.4$,可得:
$x=8 - 2.4$
$x = 5.6$
检验:
把$x = 5.6$代入原方程左边$=5.6+2.4 = 8$,右边$ = 8$,
因为左边$=$右边,所以$x = 5.6$是原方程的解。
解方程$x - 4.2 = 3.6$
解:根据等式的性质,等式两边同时加上一个数,等式仍然成立。
在方程$x - 4.2 = 3.6$两边同时加上$4.2$,可得:
$x=3.6 + 4.2$
$x = 7.8$
检验:
把$x = 7.8$代入原方程左边$=7.8-4.2 = 3.6$,右边$ = 3.6$,
因为左边$=$右边,所以$x = 7.8$是原方程的解。
综上,方程$7.6 + x = 34.5$的解为$x = 26.9$;方程$x - 74 = 102$的解为$x = 176$;方程$x + 2.4 = 8$的解为$x = 5.6$;方程$x - 4.2 = 3.6$的解为$x = 7.8$。
4. 用方程表示下面的等量关系,并求出方程的解。
(1) $ x $ 减 $ 3.2 $ 的差是 $ 4.8 $。
(2) $ x $ 加上 $ 48 $ 等于 $ 84 $。
(1) $ x $ 减 $ 3.2 $ 的差是 $ 4.8 $。
(2) $ x $ 加上 $ 48 $ 等于 $ 84 $。
答案:
4.
(1)x-3.2=4.8 x=8
(2)x+48=84 x=36
(1)x-3.2=4.8 x=8
(2)x+48=84 x=36
5. 看图列方程并解答。
(1)
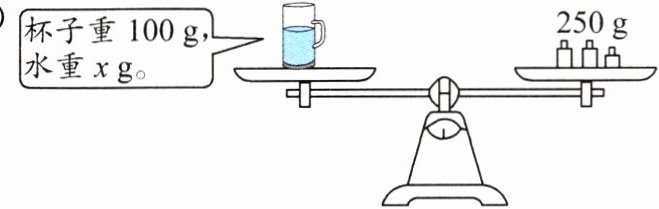
(2)

(1)

(2)

答案:
5.
(1)100+x=250 x=150
(2)y+50=120 y=70
(1)100+x=250 x=150
(2)y+50=120 y=70
6. 不计算,圈出下列每组方程中代表数值最小的字母。


答案:
6.⑥ ⑧
7. 在( )里填上适当的数,使每个方程的解都是 $ x = 4 $。
(
(
4
)$ + x = 8 $ $ x - $ (2.8
)$ = 1.2 $
答案:
7.4 2.8
查看更多完整答案,请扫码查看


