《2025年同步练习册河北教育出版社三年级数学上册冀教版》

2. 过点 $ A $ 分别画出已知直线的垂线。

答案： 过点 $A$ 作已知直线的垂线步骤如下（由于无法实际画图，以下为文字描述作答）：
对于左侧直线和点 $A$：
1. 将三角板的一条直角边与已知直线重合。
2. 移动三角板，使三角板的另一条直角边经过点 $A$。
3. 沿三角板的另一条直角边，通过点 $A$ 画直线，这条直线就是已知直线的垂线。
对于右侧直线和点 $A$：
1. 将三角板的一条直角边与已知直线重合。
2. 移动三角板，使三角板的另一条直角边经过点 $A$。
3. 沿三角板的另一条直角边，通过点 $A$ 画直线，这条直线就是已知直线的垂线。
（实际作答时应在实际试卷或答题卡上用绘图工具画出垂线）。

3. 跳远距离的测量方法：测量运动员在沙坑里留下的最近痕迹点到起跳板前沿的最短距离。请你在下图中画出这名运动员跳远的距离。

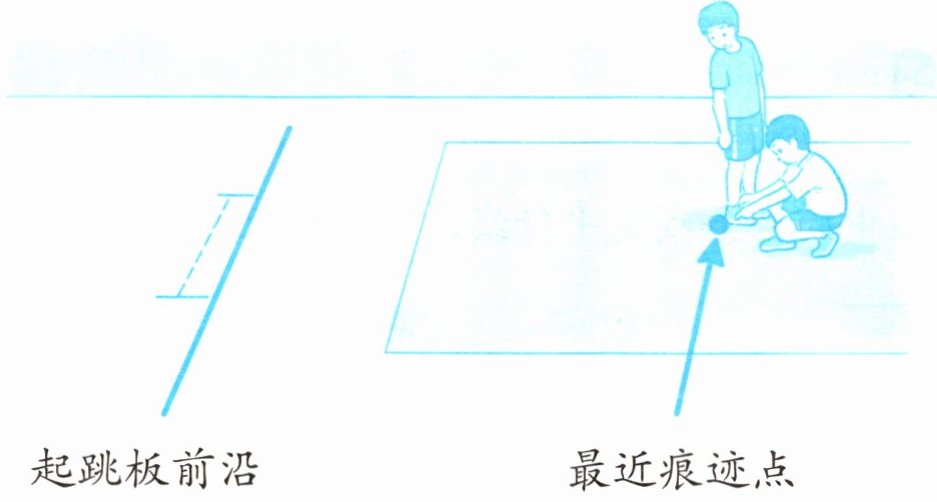
从起跳板前沿作垂线至最近痕迹点在垂线方向上的投影点（即垂足），然后用直尺连接起跳板前沿与最近痕迹点（实际测量中沿垂直方向投影后的直线距离即为跳远距离，这里作图体现为从起跳板前沿向最近痕迹点作垂线段），此垂线段即为该运动员跳远的距离（用直尺画出这条垂线段）。

答案： 从起跳板前沿作垂线至最近痕迹点在垂线方向上的投影点（即垂足），然后用直尺连接起跳板前沿与最近痕迹点（实际测量中沿垂直方向投影后的直线距离即为跳远距离，这里作图体现为从起跳板前沿向最近痕迹点作垂线段），此垂线段即为该运动员跳远的距离（用直尺画出这条垂线段）。

新农村建设改善了农村人居环境,下面是新华村一条公路的示意图,点 $ P $ 处是一个喷泉。

(1) 从喷泉修一段直达公路的小路,要使修的路最短,应该怎样修？请在图上画出来。
(2) 以喷泉所在的点 $ P $ 为起点,要修一条平行于公路 $ OA $ 且与公路 $ OB $ 相交的小路,应该怎样修？请在图上画出来。

答案：
(1) 过点 $ P $ 作垂直于公路 $ OA $ 或 $ OB $ 的垂线，修的小路为该垂线段。
(在图上画出从点 $ P $ 垂直于公路 $ OA $ 或 $ OB $ 的垂线)
(2) 过点 $ P $ 作平行于 $ OA $ 的直线，与 $ OB $ 相交。
(在图上画出过点 $ P $ 平行于 $ OA $ 的直线，与 $ OB $ 相交的直线)