第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
1.(1)5个9相加的和是( ),56里面有( )个8。
(2)两个乘数都是7,积是( );被除数和除数都是9,商是( )。
(2)两个乘数都是7,积是( );被除数和除数都是9,商是( )。
答案:
(1)45,7;
(2)49,1
(1)45,7;
(2)49,1
2. 按要求改写下面的算式。
(1)28-7-7-7-7= 0可以改写成:( )÷( )= ( )。
(2)8+8+8+8+5= ( )×( )+( )
(3)4+6+8+10+12= 8×( )
(1)28-7-7-7-7= 0可以改写成:( )÷( )= ( )。
(2)8+8+8+8+5= ( )×( )+( )
(3)4+6+8+10+12= 8×( )
答案:
(1) 28;7;4
(2) 8;4;5
(3) 5
(1) 28;7;4
(2) 8;4;5
(3) 5
3. 在( )里填合适的数。
( )+( )= 9 ( )-( )= 9
( )×( )= 9 ( )÷( )= 9
( )+( )= 9 ( )-( )= 9
( )×( )= 9 ( )÷( )= 9
答案:
1+8=9(答案不唯一);10-1=9(答案不唯一);1×9=9(或3×3=9);9÷1=9(答案不唯一)
4. 如果△表示9,那么 表示( )。
表示( )。
 表示( )。
表示( )。
答案:
1. 首先分析图形:
已知$\triangle$表示$9$,观察图形可知,该图形是由$4$个$\triangle$组成。
2. 然后计算:
那么这个图形表示的数为$4×9 = 36$。
故答案为$36$。
已知$\triangle$表示$9$,观察图形可知,该图形是由$4$个$\triangle$组成。
2. 然后计算:
那么这个图形表示的数为$4×9 = 36$。
故答案为$36$。
5. 找规律填数。
(1)81,64,49,( ),( ),( )。
(2)5,48,10,40,15,32,( ),( )。
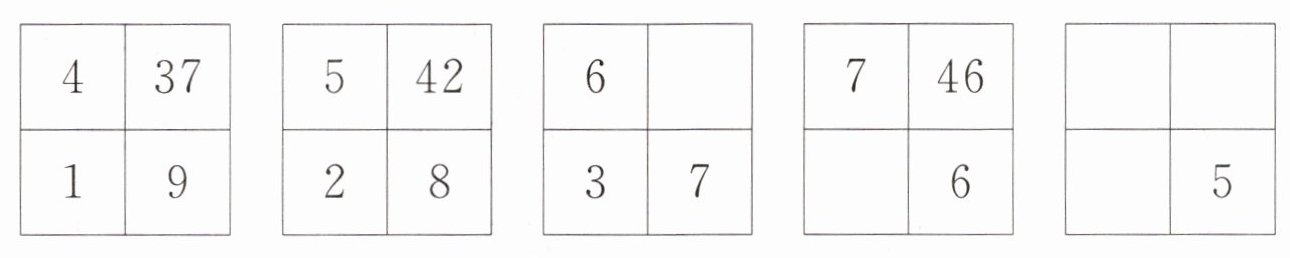
(3)
(1)81,64,49,( ),( ),( )。
(2)5,48,10,40,15,32,( ),( )。
(3)

答案:
1. (1)
分析规律:
因为$81 = 9^{2}$,$64 = 8^{2}$,$49 = 7^{2}$,所以这组数据的规律是依次为$9$、$8$、$7$、$6$、$5$、$4$的平方。
计算结果:
当$n = 6$时,$6^{2}=36$;当$n = 5$时,$5^{2}=25$;当$n = 4$时,$4^{2}=16$。
2. (2)
分析规律:
把这组数据分成两组,奇数项:$5$,$10$,$15$,规律是后一个数比前一个数大$5$;偶数项:$48$,$40$,$32$,规律是后一个数比前一个数小$8$。
计算结果:
奇数项中,$15 + 5=20$;偶数项中,$32−8 = 24$。
3. (3)
分析规律:
观察可得$4×9 + 1=37$,$5×8+2 = 42$。
计算结果:
当第一行第一个数是$6$,第二行第一个数是$3$时,$6×7+3=45$;
当第一行第一个数是$7$,第二行第二个数是$6$时,设第二行第一个数为$x$,则$7×6+x = 46$,解得$x = 4$;
设第一行第一个数为$y$,第二行第一个数为$z$,当第二行第二个数是$5$时,$y×5+z$,假设$y = 8$,$z = 0$(答案不唯一,只要满足$y×5+z$的形式,这里取$y = 8$,$z = 0$),$8×5+0 = 40$。
故答案依次为:(1)$36$,$25$,$16$;(2)$20$,$24$;(3)$45$,$4$,$8$,$0$,$40$(最后一组答案不唯一)。
分析规律:
因为$81 = 9^{2}$,$64 = 8^{2}$,$49 = 7^{2}$,所以这组数据的规律是依次为$9$、$8$、$7$、$6$、$5$、$4$的平方。
计算结果:
当$n = 6$时,$6^{2}=36$;当$n = 5$时,$5^{2}=25$;当$n = 4$时,$4^{2}=16$。
2. (2)
分析规律:
把这组数据分成两组,奇数项:$5$,$10$,$15$,规律是后一个数比前一个数大$5$;偶数项:$48$,$40$,$32$,规律是后一个数比前一个数小$8$。
计算结果:
奇数项中,$15 + 5=20$;偶数项中,$32−8 = 24$。
3. (3)
分析规律:
观察可得$4×9 + 1=37$,$5×8+2 = 42$。
计算结果:
当第一行第一个数是$6$,第二行第一个数是$3$时,$6×7+3=45$;
当第一行第一个数是$7$,第二行第二个数是$6$时,设第二行第一个数为$x$,则$7×6+x = 46$,解得$x = 4$;
设第一行第一个数为$y$,第二行第一个数为$z$,当第二行第二个数是$5$时,$y×5+z$,假设$y = 8$,$z = 0$(答案不唯一,只要满足$y×5+z$的形式,这里取$y = 8$,$z = 0$),$8×5+0 = 40$。
故答案依次为:(1)$36$,$25$,$16$;(2)$20$,$24$;(3)$45$,$4$,$8$,$0$,$40$(最后一组答案不唯一)。
6. 王老师买了二十多本练习本奖励给班上的7个同学,每个同学分得的本数同样多。王老师最多买了( )本,最少买了( )本。
答案:
因为练习本数量是二十多本,分给7个同学,每人同样多,所以想7的乘法口诀中结果在20到30之间的数。
7×3=21(本),7×4=28(本),7×5=35(本)(超过30,舍去)。
所以最多买了28本,最少买了21本。
28;21
7×3=21(本),7×4=28(本),7×5=35(本)(超过30,舍去)。
所以最多买了28本,最少买了21本。
28;21
7. 如果★+★+★+★= ▲(★不为0),那么▲÷★= ( );当▲×★= 16时,▲= ( ),★= ( )。
答案:
因为★+★+★+★=▲,所以▲是4个★相加,根据乘法的意义,▲=4×★,那么▲÷★=4。
当▲×★=16时,因为▲=4×★,所以4×★×★=16,即★×★=4。因为★不为0,二年级上册学过的乘法口诀中,2×2=4,所以★=2,那么▲=4×2=8。
4;8;2
当▲×★=16时,因为▲=4×★,所以4×★×★=16,即★×★=4。因为★不为0,二年级上册学过的乘法口诀中,2×2=4,所以★=2,那么▲=4×2=8。
4;8;2
查看更多完整答案,请扫码查看


