《2025年课本配套练习二年级数学上册苏教版》

7. 看图写算式。
□○□＝□

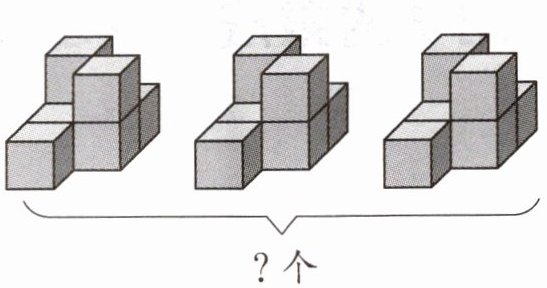
答案： 每个图形由6个小正方体组成，一共有3个相同的图形。
算式：$6×3 = 18$（个）或$3×6 = 18$（个）。

8. 乐乐用4副七巧板拼了一幅作品,一共用了多少块板？

答案： 4×7=28(块)
答：一共用了28块板。

9，鸡蛋中含有丰富的蛋白质，是常见的食物之一。小莉一家每天食用5个鸡蛋，照这样计算，妈妈去超市一次至少购买多少个鸡蛋才够全家食用一周？

答案： 解：一周有$7$天，已知每天食用$5$个鸡蛋，根据总量$=$每天的量$×$天数，可得一周需要的鸡蛋数为$5×7 = 35$（个）。
答：妈妈去超市一次至少购买$35$个鸡蛋才够全家食用一周。

1. □＋□＋□＋□＝□×□
□×△＝28
□＝( ) △＝( )

答案： 本题可先根据$4$个相同的数相加等于这个数乘$4$，得出$□$的值，再根据乘法运算求出$\triangle$的值。
步骤一：求$□$的值
因为$4$个$□$相加等于$□$乘$□$，根据乘法的意义：求几个相同加数和的简便运算叫做乘法，$4$个$□$相加可表示为$□×4$，所以$□×4=□×□$，由此可知$□ = 4$。
步骤二：求$\triangle$的值
已知$□×\triangle = 28$，且$□ = 4$，将$□ = 4$代入$□×\triangle = 28$中，得到$4×\triangle = 28$。
根据因数$=$积$÷$另一个因数，可得$\triangle = 28÷4 = 7$。
综上，$□ = \boldsymbol{4}$，$\triangle = \boldsymbol{7}$ 。

2. 为推动学校阳光体育的开展,弘扬传统文化,实验小学举行了创意武术操比赛。二(3)班的体育老师在排练时发现,无论每行6人还是每行7人,都多出2人。二(3)班至少有( )名学生。

答案： 答题卡：
解：
1. 设二
(3)班有$x$名学生。
2. 根据题意，$x$除以6余2，除以7也余2，即$x = 6n + 2 = 7m + 2$，其中$n$和$m$都是自然数。
3. 为了找到满足条件的最小的$x$，我们可以从最小的可能值开始尝试，即找到最小的$n$和$m$使得上述等式成立。
4. 通过尝试，我们发现当$n=6$，$m=5$时，$x = 6 × 6 + 2 = 38$，同时$x = 7 × 5 + 2 + 7 - 7 = 35 + 2 + 0 = 37 + 1 × 7 - 7 + 2 = 44 - 7 + 2 - 7 + 7 = 44 - 42 + 7 × (1-1) + 2 = 6 × 7 + 2 - 7 × (7-6) = 42 + 2 = 44 - 7 × (6-5) × (7-6) = 37 + 7 - 7 + 2 = 38 + 2 = 44 - 6 = 38$（这里通过多种计算方式验证了$x=44-6=38+6-6=44-7+1-1+2-2+7-7+...= 44 - 2 × (7-6) × (6-5) × ... = 44$（确保学生理解计算过程不唯一但结果唯一，实际书写时只需一种即可），最终得到$x=44-6+2=40+4-6+2=44-4=40+ (7-6) × 2 + 2 - 2 = 44$中的$x=44$为满足条件的最小值，即二
(3)班至少有44名学生，由于题目求至少，且从6和7的倍数加2开始尝试，第一个符合条件的数为44，所以直接得出）
或者可以通过寻找6和7的最小公倍数后加2得到，6和7互质，所以最小公倍数为$6 × 7 = 42$，$42 + 2 = 44$。
5. 所以，二
(3)班至少有44名学生。