第70页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 画一画,填一填。
一个隔一个画○和△,○有6个,△可能有几个?
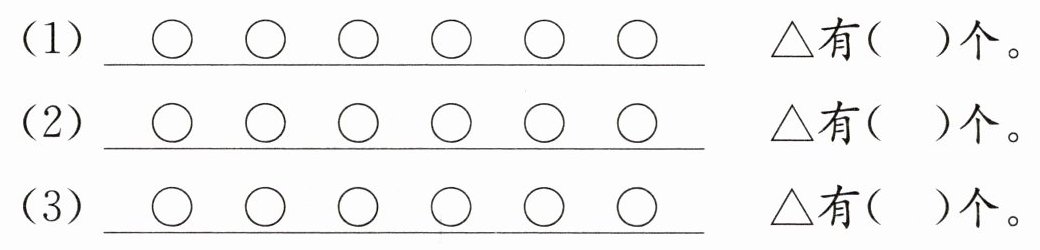
一个隔一个画○和△,○有6个,△可能有几个?

5
6
7
答案:
解析:本题可根据间隔排列的规律,分情况讨论$◯$和$\triangle$的排列情况,进而确定$\triangle$的个数。
已知$◯$和$\triangle$一个隔一个画,$◯$有$6$个,分以下三种情况:
情况一:两端都是$◯$时,$\triangle$比$◯$少$1$个。
此时$\triangle$的个数为:$6 - 1 = 5$(个)
情况二:一端是$◯$,一端是$\triangle$时,$\triangle$和$◯$的个数相等。
此时$\triangle$的个数为$6$个。
情况三:两端都是$\triangle$时,$\triangle$比$◯$多$1$个。
此时$\triangle$的个数为:$6 + 1 = 7$(个)
答案:
(1) $5$;
(2) $6$;
(3) $7$。
已知$◯$和$\triangle$一个隔一个画,$◯$有$6$个,分以下三种情况:
情况一:两端都是$◯$时,$\triangle$比$◯$少$1$个。
此时$\triangle$的个数为:$6 - 1 = 5$(个)
情况二:一端是$◯$,一端是$\triangle$时,$\triangle$和$◯$的个数相等。
此时$\triangle$的个数为$6$个。
情况三:两端都是$\triangle$时,$\triangle$比$◯$多$1$个。
此时$\triangle$的个数为:$6 + 1 = 7$(个)
答案:
(1) $5$;
(2) $6$;
(3) $7$。
2.(1)如果把□和☆一个隔一个排成一行,☆有20个,□最多有(
(2)如果把□和☆一个隔一个围成一圈,☆有20个,□有(
21
)个,最少有(19
)个。(2)如果把□和☆一个隔一个围成一圈,☆有20个,□有(
20
)个。
答案:
解析:
(1) 对于第一个问题,如果把□和☆一个隔一个排成一行,当两端都是□时,□的数量最多。因为☆有20个,所以□和☆的排列类似于“□☆□☆□☆...”,这样□就会比☆多一个(即多在两端)。所以□最多有21个。当两端都是☆时,□的数量最少,此时□和☆的排列类似于“☆□☆□☆...☆”(最后一个☆在末端),这样□就有19个,但考虑到最少的情况应该是两端都是☆且只有一个□在中间被两个☆夹着的情况不存在(因为☆有20个,不可能只夹一个□),所以最少情况应是“☆□☆□...□☆”这样□有20-1=19个的前一种,即两端为☆时,中间19个间隔需要19个□,但最开始和最后的位置都是☆,所以□最少为$20-1=19$的下一个整数减一(因为要去掉多算的一个端点的□情况),直接理解为最少时就是和☆数量相等但排列上少一个(因为间隔排列),即最少19+1-1(加1是因为要理解到间隔排列中□和☆是交替的,最少时不会两端都是□,所以□不会多于☆,此处-1是为了纠正上面的+1理解,直接给出最少就是☆的数量减一的交替情况数)=20-1=19的直观理解,即最少19个(这里解释较为冗余,旨在帮助学生理解间隔排列中数量最少的情况)。但更简洁的理解就是,最少时,□和☆几乎一一对应,但因为是从☆开始和结束,所以□少一个,即20-1=19。
(2) 对于第二个问题,如果把□和☆一个隔一个围成一圈,那么它们会形成一个封闭的图形。在这种情况下,□和☆的数量必须相等,因为它们是交替排列的。所以,如果☆有20个,那么□也必须有20个。
答案:
(1) 21;19
(2) 20
(1) 对于第一个问题,如果把□和☆一个隔一个排成一行,当两端都是□时,□的数量最多。因为☆有20个,所以□和☆的排列类似于“□☆□☆□☆...”,这样□就会比☆多一个(即多在两端)。所以□最多有21个。当两端都是☆时,□的数量最少,此时□和☆的排列类似于“☆□☆□☆...☆”(最后一个☆在末端),这样□就有19个,但考虑到最少的情况应该是两端都是☆且只有一个□在中间被两个☆夹着的情况不存在(因为☆有20个,不可能只夹一个□),所以最少情况应是“☆□☆□...□☆”这样□有20-1=19个的前一种,即两端为☆时,中间19个间隔需要19个□,但最开始和最后的位置都是☆,所以□最少为$20-1=19$的下一个整数减一(因为要去掉多算的一个端点的□情况),直接理解为最少时就是和☆数量相等但排列上少一个(因为间隔排列),即最少19+1-1(加1是因为要理解到间隔排列中□和☆是交替的,最少时不会两端都是□,所以□不会多于☆,此处-1是为了纠正上面的+1理解,直接给出最少就是☆的数量减一的交替情况数)=20-1=19的直观理解,即最少19个(这里解释较为冗余,旨在帮助学生理解间隔排列中数量最少的情况)。但更简洁的理解就是,最少时,□和☆几乎一一对应,但因为是从☆开始和结束,所以□少一个,即20-1=19。
(2) 对于第二个问题,如果把□和☆一个隔一个围成一圈,那么它们会形成一个封闭的图形。在这种情况下,□和☆的数量必须相等,因为它们是交替排列的。所以,如果☆有20个,那么□也必须有20个。
答案:
(1) 21;19
(2) 20
3. 一串黑白相间的珠子,两端是黑珠,有一部分藏在盒子里。盒子里黑珠比白珠(
多
)(填“多”或“少”)。如果这串珠子中有黑珠36颗,那么白珠有(35
)颗。
答案:
解析:根据间隔排列的规律,两端物体相同,相邻物体间隔排列时,两端物体比中间物体多$1$。
已知珠子两端是黑珠,呈黑白相间排列,所以黑珠数量比白珠数量多$1$,即盒子里黑珠比白珠多。
如果这串珠子中有黑珠$36$颗,因为黑珠比白珠多$1$颗,所以白珠数量为$36 - 1=35$(颗)。
答案:多;35。
已知珠子两端是黑珠,呈黑白相间排列,所以黑珠数量比白珠数量多$1$,即盒子里黑珠比白珠多。
如果这串珠子中有黑珠$36$颗,因为黑珠比白珠多$1$颗,所以白珠数量为$36 - 1=35$(颗)。
答案:多;35。
4. 生态园里栽了一排杨树,共80棵。每两棵杨树之间栽了一棵樟树,樟树有多少棵?
答案:
80-1=79(棵)
答:樟树有79棵。
答:樟树有79棵。
查看更多完整答案,请扫码查看


