《2025年新课程学习与测评同步学习六年级数学上册苏教版》

小试身手 1. (1) 下图中的正方体的底面积是 0.36 平方分米,它的体积是多少立方分米？

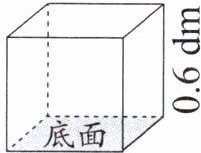
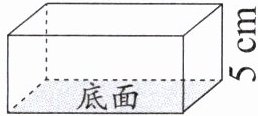
(2) 下图中的长方体的底面积是 70 平方厘米,它的体积是多少立方厘米？

答案： 1.
(1)$0.36×0.6=0.216$(立方分米)
(2)$70×5=350$(立方厘米)

2. 每课速算。
$ 0.75×10 = $ $ 10 - 1.09 = $
$ 1.3 + 8.7 = $ $ 5.1÷1.7 = $
$ \frac{3}{4} + \frac{1}{6} = $ $ 1 - \frac{1}{5} = $

答案： 2.7.5 8.91 10 3 $\frac {11}{12}$ $\frac {4}{5}$

3. 填空题。
(1) 学校图书室有一排高 1.5 米的储物柜,占地面积是 2.4 平方米。这排储物柜所占空间是( )立方米。
(2) 在一个长 9 分米、宽 8 分米、高 6 分米的长方体纸箱里(不考虑纸箱纸板厚度),放进棱长为 2 分米的正方体模型,最多可以放( )个。
(3) 把 5 升水倒进一个棱长为 2 分米的正方体容器中,水的高度是( )分米；如果要装满这个容器,还需倒进( )升水。

答案： 3.
(1)3.6
(2)48
(3)1.25 3

4. 如下图,这根木料的长是 5 米,它的体积是多少立方米？

答案： 4.$0.06×5=0.3$(立方米)

5. 把一块棱长为 3 分米的正方体铁块熔铸成一块底面积是 5.4 平方分米的长方体铁块。这块长方体铁块的高是多少分米？

答案： 5.$(3×3×3)÷5.4=5$(分米)

6. 一个长方体(如右图),如果高增加 3 厘米,就变成一个正方体,这时表面积比原来增加 72 平方厘米。原来这个长方体的体积是多少立方厘米？
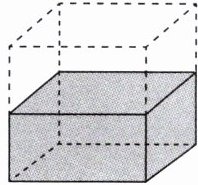
锦囊妙计 表面积增加的部分是四个完全一样的长方形的面积的和,可以先求出每个长方形的面积,再求出每个长方形的长。

答案： 6.$72÷4÷3=6$(厘米) $6×6×(6-3)=108$(立方厘米)